© | Dror Bar-Natan: The Knot Atlas: The Rolfsen Knot Table:

931 933

KnotPlot

This page is passe. Go here instead!    The Alternating Knot 932    Visit 932's page at the Knot Server (KnotPlot driven, includes 3D interactive images!) Visit 932's page at Knotilus! Acknowledgement

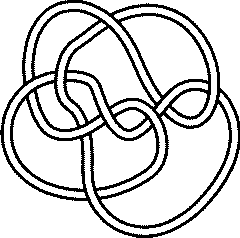KnotPlot

PD Presentation:

X1425 X13,18,14,1 X3948 X9,3,10,2 X7,15,8,14 X15,11,16,10 X5,12,6,13 X11,17,12,16 X17,7,18,6

Gauss Code:

{-1, 4, -3, 1, -7, 9, -5, 3, -4, 6, -8, 7, -2, 5, -6, 8, -9, 2}

DT (Dowker-Thistlethwaite) Code:

4 8 12 14 2 16 18 10 6

Minimum Braid Representative: Length is 9, width is 4 Braid index is 4

A Morse Link Presentation:

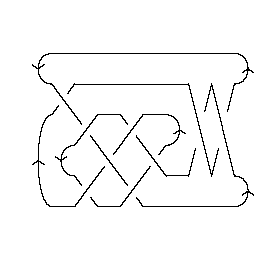
3D Invariants:

Symmetry Type Unknotting Number 3-Genus Bridge/Super Bridge Index Nakanishi Index Chiral 2 3 3 / 4--6 1

Alexander Polynomial:

t-3 - 6t-2 + 14t-1 - 17 + 14t - 6t2 + t3

Conway Polynomial:

1 - z2 + z6

Other knots with the same Alexander/Conway Polynomial:

{K11n52, K11n124, ...}

Determinant and Signature:

{59, 2}

Jones Polynomial:

- q-2 + 4q-1 - 6 + 9q - 10q2 + 10q3 - 9q4 + 6q5 - 3q6 + q7

Other knots (up to mirrors) with the same Jones Polynomial:

{...}

A2 (sl(3)) Invariant:

- q-6 + 2q-4 + 1 + 3q2 - 2q4 + 2q6 - 2q8 - 2q14 + 2q16 - q18 + q22

HOMFLY-PT Polynomial:

a-6 + a-6z2 - 2a-4 - 4a-4z2 - 2a-4z4 + a-2 + 3a-2z2 + 3a-2z4 + a-2z6 + 1 - z2 - z4

Kauffman Polynomial:

- a-8z2 + a-8z4 + a-7z - 3a-7z3 + 3a-7z5 - a-6 + 4a-6z2 - 6a-6z4 + 5a-6z6 + 2a-5z3 - 5a-5z5 + 5a-5z7 - 2a-4 + 12a-4z2 - 18a-4z4 + 7a-4z6 + 2a-4z8 - 2a-3z + 9a-3z3 - 18a-3z5 + 10a-3z7 - a-2 + 10a-2z2 - 19a-2z4 + 6a-2z6 + 2a-2z8 - a-1z + 3a-1z3 - 9a-1z5 + 5a-1z7 + 1 + 3z2 - 8z4 + 4z6 - az3 + az5

V2 and V3, the type 2 and 3 Vassiliev invariants:

{-1, -2}

Khovanov Homology: (The squares with yellow highlighting are those on the "critical diagonals", where j-2r=s+1 or j-2r=s+1, where s=2 is the signature of 932. Nonzero entries off the critical diagonals (if any exist) are highlighted in red.)

trqj r = -3 r = -2 r = -1 r = 0 r = 1 r = 2 r = 3 r = 4 r = 5 r = 6 j = 15                   1 j = 13                 2   j = 11               4 1   j = 9             5 2     j = 7           5 4       j = 5         5 5         j = 3       4 5           j = 1     3 6             j = -1   1 3               j = -3   3                 j = -5 1

n	Coloured Jones Polynomial (in the (n+1)-dimensional representation of sl(2))
2	q-7 - 4q-6 + q-5 + 14q-4 - 19q-3 - 9q-2 + 46q-1 - 32 - 37q + 82q2 - 32q3 - 69q4 + 102q5 - 20q6 - 87q7 + 97q8 - 4q9 - 80q10 + 67q11 + 8q12 - 50q13 + 29q14 + 8q15 - 18q16 + 7q17 + 2q18 - 3q19 + q20
3	- q-15 + 4q-14 - q-13 - 9q-12 - 4q-11 + 22q-10 + 21q-9 - 44q-8 - 47q-7 + 52q-6 + 105q-5 - 56q-4 - 168q-3 + 26q-2 + 248q-1 + 18 - 306q - 103q2 + 368q3 + 180q4 - 389q5 - 276q6 + 405q7 + 353q8 - 392q9 - 425q10 + 371q11 + 472q12 - 331q13 - 499q14 + 275q15 + 503q16 - 210q17 - 475q18 + 134q19 + 426q20 - 69q21 - 344q22 + 8q23 + 259q24 + 25q25 - 175q26 - 34q27 + 101q28 + 32q29 - 53q30 - 20q31 + 25q32 + 9q33 - 11q34 - 2q35 + 3q36 + 2q37 - 3q38 + q39
4	q-26 - 4q-25 + q-24 + 9q-23 - q-22 + q-21 - 34q-20 - 6q-19 + 51q-18 + 33q-17 + 39q-16 - 146q-15 - 116q-14 + 87q-13 + 171q-12 + 286q-11 - 258q-10 - 441q-9 - 137q-8 + 270q-7 + 900q-6 - 31q-5 - 782q-4 - 805q-3 - 76q-2 + 1619q-1 + 728 - 667q - 1637q2 - 1032q3 + 1947q4 + 1710q5 + 51q6 - 2162q7 - 2243q8 + 1725q9 + 2467q10 + 1045q11 - 2243q12 - 3257q13 + 1195q14 + 2842q15 + 1935q16 - 2023q17 - 3875q18 + 575q19 + 2870q20 + 2584q21 - 1581q22 - 4058q23 - 92q24 + 2518q25 + 2926q26 - 876q27 - 3700q28 - 744q29 + 1724q30 + 2802q31 - 33q32 - 2744q33 - 1097q34 + 696q35 + 2099q36 + 552q37 - 1487q38 - 931q39 - 64q40 + 1115q41 + 593q42 - 516q43 - 455q44 - 268q45 + 377q46 + 310q47 - 102q48 - 105q49 - 150q50 + 79q51 + 87q52 - 22q53 + q54 - 40q55 + 14q56 + 15q57 - 10q58 + 5q59 - 6q60 + 3q61 + 2q62 - 3q63 + q64
5	- q-40 + 4q-39 - q-38 - 9q-37 + q-36 + 4q-35 + 11q-34 + 19q-33 - q-32 - 54q-31 - 52q-30 + 3q-29 + 81q-28 + 144q-27 + 81q-26 - 123q-25 - 331q-24 - 262q-23 + 99q-22 + 522q-21 + 656q-20 + 189q-19 - 720q-18 - 1269q-17 - 754q-16 + 607q-15 + 1903q-14 + 1886q-13 - 10q-12 - 2453q-11 - 3277q-10 - 1320q-9 + 2365q-8 + 4880q-7 + 3414q-6 - 1530q-5 - 6075q-4 - 6065q-3 - 448q-2 + 6687q-1 + 8853 + 3275q - 6139q2 - 11406q3 - 6881q4 + 4705q5 + 13250q6 + 10566q7 - 2159q8 - 14289q9 - 14220q10 - 768q11 + 14444q12 + 17236q13 + 4052q14 - 13903q15 - 19764q16 - 7094q17 + 12916q18 + 21529q19 + 9928q20 - 11685q21 - 22814q22 - 12308q23 + 10339q24 + 23593q25 + 14376q26 - 8927q27 - 23994q28 - 16121q29 + 7369q30 + 23966q31 + 17645q32 - 5581q33 - 23432q34 - 18914q35 + 3477q36 + 22257q37 + 19787q38 - 1026q39 - 20281q40 - 20169q41 - 1572q42 + 17518q43 + 19690q44 + 4127q45 - 13982q46 - 18374q47 - 6238q48 + 10142q49 + 16014q50 + 7577q51 - 6252q52 - 12993q53 - 7951q54 + 2926q55 + 9628q56 + 7327q57 - 458q58 - 6374q59 - 6020q60 - 1007q61 + 3700q62 + 4399q63 + 1513q64 - 1766q65 - 2825q66 - 1439q67 + 624q68 + 1597q69 + 1058q70 - 93q71 - 776q72 - 641q73 - 76q74 + 313q75 + 331q76 + 96q77 - 121q78 - 147q79 - 40q80 + 31q81 + 42q82 + 35q83 - 12q84 - 27q85 + 4q86 + 4q87 - 4q88 + 6q89 + q90 - 6q91 + 3q92 + 2q93 - 3q94 + q95
6	q-57 - 4q-56 + q-55 + 9q-54 - q-53 - 4q-52 - 16q-51 + 4q-50 - 12q-49 + 4q-48 + 73q-47 + 27q-46 - 10q-45 - 110q-44 - 77q-43 - 118q-42 - 11q-41 + 324q-40 + 334q-39 + 233q-38 - 245q-37 - 437q-36 - 888q-35 - 660q-34 + 512q-33 + 1315q-32 + 1798q-31 + 799q-30 - 291q-29 - 2765q-28 - 3733q-27 - 1819q-26 + 1259q-25 + 4916q-24 + 5656q-23 + 4520q-22 - 2333q-21 - 8666q-20 - 10190q-19 - 6096q-18 + 3608q-17 + 12261q-16 + 17942q-15 + 9095q-14 - 6222q-13 - 20201q-12 - 24431q-11 - 13086q-10 + 7842q-9 + 32323q-8 + 34152q-7 + 16165q-6 - 15598q-5 - 42500q-4 - 45896q-3 - 20644q-2 + 28574q-1 + 58074 + 56492q + 16095q2 - 39655q3 - 77020q4 - 68014q5 - 4087q6 + 59951q7 + 94702q8 + 66676q9 - 7813q10 - 86365q11 - 112907q12 - 54804q13 + 34544q14 + 112292q15 + 114625q16 + 40159q17 - 71117q18 - 138786q19 - 102796q20 - 4583q21 + 108204q22 + 145596q23 + 85033q24 - 44187q25 - 145520q26 - 135979q27 - 40914q28 + 93712q29 + 159998q30 + 117220q31 - 18612q32 - 142225q33 - 155281q34 - 67952q35 + 78198q36 + 165053q37 + 138590q38 + 2412q39 - 135004q40 - 166670q41 - 89099q42 + 61828q43 + 164354q44 + 154579q45 + 23969q46 - 121540q47 - 171876q48 - 109645q49 + 38125q50 + 153502q51 + 165275q52 + 51048q53 - 94293q54 - 164451q55 - 127781q56 + 2940q57 + 124029q58 + 161902q59 + 79231q60 - 50512q61 - 134970q62 - 131885q63 - 35893q64 + 74956q65 + 134097q66 + 93434q67 - 1980q68 - 84404q69 - 110550q70 - 59742q71 + 21832q72 + 84964q73 + 81352q74 + 29748q75 - 31404q76 - 68728q77 - 56251q78 - 12472q79 + 35307q80 + 49646q81 + 33577q82 + 1648q83 - 27884q84 - 34059q85 - 19619q86 + 5530q87 + 19301q88 + 20073q89 + 9892q90 - 5042q91 - 12929q92 - 11755q93 - 2908q94 + 3609q95 + 7019q96 + 5982q97 + 1130q98 - 2719q99 - 4001q100 - 1953q101 - 320q102 + 1288q103 + 1910q104 + 889q105 - 198q106 - 838q107 - 451q108 - 325q109 + 45q110 + 387q111 + 227q112 + 21q113 - 136q114 - 17q115 - 75q116 - 36q117 + 65q118 + 31q119 + 4q120 - 30q121 + 17q122 - 6q123 - 15q124 + 12q125 + 2q126 + q127 - 6q128 + 3q129 + 2q130 - 3q131 + q132
7	- q-77 + 4q-76 - q-75 - 9q-74 + q-73 + 4q-72 + 16q-71 + q-70 - 11q-69 + 9q-68 - 23q-67 - 48q-66 - 20q-65 + 22q-64 + 115q-63 + 115q-62 + 17q-61 + 9q-60 - 175q-59 - 325q-58 - 297q-57 - 146q-56 + 403q-55 + 771q-54 + 753q-53 + 602q-52 - 242q-51 - 1286q-50 - 1942q-49 - 2123q-48 - 545q-47 + 1738q-46 + 3582q-45 + 4792q-44 + 3232q-43 - 389q-42 - 4946q-41 - 9313q-40 - 9107q-39 - 4078q-38 + 4079q-37 + 13731q-36 + 18046q-35 + 14636q-34 + 3251q-33 - 15014q-32 - 29028q-31 - 31954q-30 - 20034q-29 + 7106q-28 + 35681q-27 + 53589q-26 + 49846q-25 + 16850q-24 - 30554q-23 - 73055q-22 - 89229q-21 - 60293q-20 + 2657q-19 + 77577q-18 + 130419q-17 + 123208q-16 + 54368q-15 - 54934q-14 - 158264q-13 - 194768q-12 - 141472q-11 - 7231q-10 + 155997q-9 + 259807q-8 + 249742q-7 + 110713q-6 - 108674q-5 - 297100q-4 - 362267q-3 - 249838q-2 + 10048q-1 + 289913 + 456726q + 407418q2 + 136576q3 - 227070q4 - 514084q5 - 562486q6 - 315866q7 + 110089q8 + 519701q9 + 692548q10 + 508938q11 + 51082q12 - 471908q13 - 783220q14 - 692579q15 - 237132q16 + 376048q17 + 826008q18 + 850811q19 + 429692q20 - 247638q21 - 824806q22 - 972385q23 - 609132q24 + 102804q25 + 786917q26 + 1055734q27 + 765105q28 + 41884q29 - 726912q30 - 1104431q31 - 890498q32 - 174596q33 + 656067q34 + 1126789q35 + 986871q36 + 288357q37 - 585697q38 - 1131910q39 - 1057824q40 - 381833q41 + 521580q42 + 1128133q43 + 1110493q44 + 457494q45 - 466067q46 - 1120943q47 - 1151735q48 - 521047q49 + 417185q50 + 1113068q51 + 1187340q52 + 579062q53 - 369907q54 - 1103145q55 - 1220714q56 - 638364q57 + 317114q58 + 1086812q59 + 1252009q60 + 703612q61 - 251190q62 - 1056639q63 - 1277125q64 - 776310q65 + 165485q66 + 1003430q67 + 1288481q68 + 853575q69 - 56996q70 - 919017q71 - 1275408q72 - 926425q73 - 72075q74 + 797405q75 + 1226367q76 + 983011q77 + 213254q78 - 640204q79 - 1133393q80 - 1007602q81 - 350667q82 + 454830q83 + 993376q84 + 988216q85 + 466948q86 - 258583q87 - 814225q88 - 917388q89 - 543085q90 + 72472q91 + 610234q92 + 798380q93 + 568344q94 + 81887q95 - 404663q96 - 644240q97 - 539814q98 - 188080q99 + 220283q100 + 474676q101 + 466810q102 + 240410q103 - 75419q104 - 313090q105 - 366766q106 - 243093q107 - 20488q108 + 177698q109 + 259411q110 + 210456q111 + 69749q112 - 79204q113 - 163410q114 - 159932q115 - 81855q116 + 18600q117 + 89212q118 + 107217q119 + 71544q120 + 11067q121 - 40070q122 - 63534q123 - 51986q124 - 19664q125 + 12676q126 + 32798q127 + 32371q128 + 17614q129 - 342q130 - 14436q131 - 17673q132 - 12095q133 - 3214q134 + 5285q135 + 8395q136 + 6743q137 + 3115q138 - 1292q139 - 3455q140 - 3397q141 - 2076q142 + 214q143 + 1318q144 + 1347q145 + 1000q146 + 145q147 - 334q148 - 553q149 - 557q150 - 44q151 + 179q152 + 148q153 + 151q154 + 25q155 + 18q156 - 44q157 - 122q158 + 39q160 + 13q161 + 10q162 - 14q163 + 14q164 + 7q165 - 25q166 + q167 + 8q168 + 2q169 + q170 - 6q171 + 3q172 + 2q173 - 3q174 + q175

Computer Talk. The data above can be recomputed by Mathematica using the package KnotTheory`. Following setup, the sample Mathematica session below reproduces most of the above data (Mathematica system prompts in blue, human input in red, Mathematica output in black):

In[1]:=	<< KnotTheory`
Loading KnotTheory` (version of August 30, 2005, 10:15:35)...
In[2]:=	PD[Knot[9, 32]]
Out[2]=	PD[X[1, 4, 2, 5], X[13, 18, 14, 1], X[3, 9, 4, 8], X[9, 3, 10, 2], > X[7, 15, 8, 14], X[15, 11, 16, 10], X[5, 12, 6, 13], X[11, 17, 12, 16], > X[17, 7, 18, 6]]
In[3]:=	GaussCode[Knot[9, 32]]
Out[3]=	GaussCode[-1, 4, -3, 1, -7, 9, -5, 3, -4, 6, -8, 7, -2, 5, -6, 8, -9, 2]
In[4]:=	DTCode[Knot[9, 32]]
Out[4]=	DTCode[4, 8, 12, 14, 2, 16, 18, 10, 6]
In[5]:=	br = BR[Knot[9, 32]]
Out[5]=	BR[4, {1, 1, -2, 1, -2, 1, 3, -2, 3}]
In[6]:=	{First[br], Crossings[br]}
Out[6]=	{4, 9}
In[7]:=	BraidIndex[Knot[9, 32]]
Out[7]=	4
In[8]:=	Show[DrawMorseLink[Knot[9, 32]]]
Out[8]=	-Graphics-
In[9]:=	#[Knot[9, 32]]& /@ {SymmetryType, UnknottingNumber, ThreeGenus, BridgeIndex, SuperBridgeIndex, NakanishiIndex}
Out[9]=	{Chiral, 2, 3, 3, {4, 6}, 1}
In[10]:=	alex = Alexander[Knot[9, 32]][t]
Out[10]=	-3 6 14 2 3 -17 + t - -- + -- + 14 t - 6 t + t 2 t t
In[11]:=	Conway[Knot[9, 32]][z]
Out[11]=	2 6 1 - z + z
In[12]:=	Select[AllKnots[], (alex === Alexander[#][t])&]
Out[12]=	{Knot[9, 32], Knot[11, NonAlternating, 52], Knot[11, NonAlternating, 124]}
In[13]:=	{KnotDet[Knot[9, 32]], KnotSignature[Knot[9, 32]]}
Out[13]=	{59, 2}
In[14]:=	Jones[Knot[9, 32]][q]
Out[14]=	-2 4 2 3 4 5 6 7 -6 - q + - + 9 q - 10 q + 10 q - 9 q + 6 q - 3 q + q q
In[15]:=	Select[AllKnots[], (J === Jones[#][q] || (J /. q-> 1/q) === Jones[#][q])&]
Out[15]=	{Knot[9, 32]}
In[16]:=	A2Invariant[Knot[9, 32]][q]
Out[16]=	-6 2 2 4 6 8 14 16 18 22 1 - q + -- + 3 q - 2 q + 2 q - 2 q - 2 q + 2 q - q + q 4 q
In[17]:=	HOMFLYPT[Knot[9, 32]][a, z]
Out[17]=	2 2 2 4 4 6 -6 2 -2 2 z 4 z 3 z 4 2 z 3 z z 1 + a - -- + a - z + -- - ---- + ---- - z - ---- + ---- + -- 4 6 4 2 4 2 2 a a a a a a a
In[18]:=	Kauffman[Knot[9, 32]][a, z]
Out[18]=	2 2 2 2 3 -6 2 -2 z 2 z z 2 z 4 z 12 z 10 z 3 z 1 - a - -- - a + -- - --- - - + 3 z - -- + ---- + ----- + ----- - ---- + 4 7 3 a 8 6 4 2 7 a a a a a a a a 3 3 3 4 4 4 4 5 2 z 9 z 3 z 3 4 z 6 z 18 z 19 z 3 z > ---- + ---- + ---- - a z - 8 z + -- - ---- - ----- - ----- + ---- - 5 3 a 8 6 4 2 7 a a a a a a a 5 5 5 6 6 6 7 7 5 z 18 z 9 z 5 6 5 z 7 z 6 z 5 z 10 z > ---- - ----- - ---- + a z + 4 z + ---- + ---- + ---- + ---- + ----- + 5 3 a 6 4 2 5 3 a a a a a a a 7 8 8 5 z 2 z 2 z > ---- + ---- + ---- a 4 2 a a
In[19]:=	{Vassiliev[2][Knot[9, 32]], Vassiliev[3][Knot[9, 32]]}
Out[19]=	{-1, -2}
In[20]:=	Kh[Knot[9, 32]][q, t]
Out[20]=	3 1 3 1 3 3 q 3 5 5 2 6 q + 4 q + ----- + ----- + ---- + --- + --- + 5 q t + 5 q t + 5 q t + 5 3 3 2 2 q t t q t q t q t 7 2 7 3 9 3 9 4 11 4 11 5 13 5 > 5 q t + 4 q t + 5 q t + 2 q t + 4 q t + q t + 2 q t + 15 6 > q t
In[21]:=	ColouredJones[Knot[9, 32], 2][q]
Out[21]=	-7 4 -5 14 19 9 46 2 3 4 -32 + q - -- + q + -- - -- - -- + -- - 37 q + 82 q - 32 q - 69 q + 6 4 3 2 q q q q q 5 6 7 8 9 10 11 12 13 > 102 q - 20 q - 87 q + 97 q - 4 q - 80 q + 67 q + 8 q - 50 q + 14 15 16 17 18 19 20 > 29 q + 8 q - 18 q + 7 q + 2 q - 3 q + q

Dror Bar-Natan: The Knot Atlas: The Rolfsen Knot Table: The Knot 932

931 933