© | Dror Bar-Natan: Knot Atlas: KnotTheory`:               This page is passe. Go here instead!

7.10 Finite Type (Vassiliev) Invariants

In[1]

In[2]:= ?Vassiliev
Vassiliev[2][K] computes the (standardly normalized) type 2 Vassiliev invariant of the knot K, i.e., the coefficient of z^2 in Conway[K][z]. Vassiliev[3][K] computes the (standardly normalized) type 3 Vassiliev invariant of the knot K, i.e., 3J''(1)-(1/36)J'''(1) where J is the Jones polynomial of K.

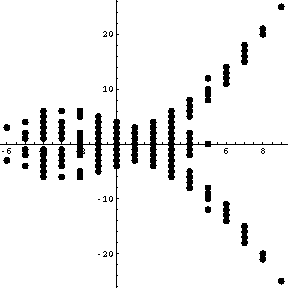
Thus, for example, let us reproduce Willerton's ``fish'' [Wi1,Wi2], the result of plotting the values of $V_2(K)$ against the values of $\pm V_3(K)$, where $V_2(K)$ is the (standardly normalized) type 2 invariant of $K$, $V_3(K)$ is the (standardly normalized) type 3 invariant of $K$, and where $K$ runs over a set of knots with equal crossing numbers (10, in the example below):

In[3]:=	ListPlot[ Join @@ Table[ K = Knot[10, k] ; v2 = Vassiliev[2][K]; v3 = Vassiliev[3][K]; {{v2, v3}, {v2, -v3}}, {k, 165} ], PlotStyle -> PointSize[0.02], PlotRange -> All, AspectRatio -> 1 ]
Out[3]=	-Graphics-