© | Dror Bar-Natan: Knot Atlas: KnotTheory`:               This page is passe. Go here instead!

7.6 The Coloured Jones Polynomials

KnotTheory` can compute the coloured Jones polynomial of braid closures, using the same formulas as in [GL]:

In[1]

In[2]:= ?ColouredJones
ColouredJones[br, n][q] computes the coloured Jones polynomial of the closure of the braid br in colour n (i.e., in the (n+1)-dimensional representation) and with respect to the variable q. ColouredJones[K, n][q] does the same for knots for which a braid representative is known to this program.

In[3]:= ColouredJones::about
The ColouredJones program was written jointly with Stavros Garoufalidis, based on formulas provided to us by Thang Le.

In[4]:= Options[ColouredJones]
{Compute -> True}

Thus, for example, here's the coloured Jones polynomial of the knot $4_1$ in the 4-dimensional representation of $sl(2)$:

In[5]:=	ColouredJones[Knot[4, 1], 3][q]
Out[5]=	-12 -11 -10 2 2 3 3 2 4 6 8 3 + q - q - q + -- - -- + -- - -- - 3 q + 3 q - 2 q + 2 q - 8 6 4 2 q q q q 10 11 12 > q - q + q

And here's the coloured Jones polynomial of the same knot in the two dimensional representation of $sl(2)$; this better be equal to the ordinary Jones polynomial of $4_1$!

In[6]:=	ColouredJones[Knot[4, 1], 1][q]
Out[6]=	-2 1 2 1 + q - - - q + q q

In[7]:=	Jones[Knot[4, 1]][q]
Out[7]=	-2 1 2 1 + q - - - q + q q

In[8]:= ?CJ`Summand
CJ`Summand[br, n] returned a pair {s, vars} where s is the summand in the the big sum that makes up ColouredJones[br, n][q] and where vars is the list of variables that need to be summed over (from 0 to n) to get ColouredJones[br, n][q]. CJ`Summand[K, n] is the same for knots for which a braid representative is known to this program.

The coloured Jones polynomial of $3_1$ is computed via a single summation. Indeed,

In[9]:=	s = CJ`Summand[Mirror[Knot[3, 1]], n]
Out[9]=	(3 n)/2 + n CJ`k[1] + (-n + 2 CJ`k[1])/2 1 {CJ`q qBinomial[0, 0, ----] CJ`q 1 1 > qBinomial[CJ`k[1], 0, ----] qBinomial[CJ`k[1], CJ`k[1], ----] CJ`q CJ`q n 1 n 1 > qPochhammer[CJ`q , ----, 0] qPochhammer[CJ`q , ----, CJ`k[1]] CJ`q CJ`q n - CJ`k[1] 1 > qPochhammer[CJ`q , ----, 0], {CJ`k[1]}} CJ`q

The symbols in the above formula require a definition:

In[10]:= ?qPochhammer
qPochhammer[a, q, k] represents the q-shifted factorial of a in base q with index k. See Eric Weisstein's
http://mathworld.wolfram.com/q-PochhammerSymbol.html and Axel Riese's
www.risc.uni-linz.ac.at/research/combinat/risc/software/qMultiSum/

In[11]:= ?qBinomial
qBinomial[n, k, q] represents the q-binomial coefficient of n and k in base q. For k<0 it is 0; otherwise it is
qPochhammer[q^(n-k+1), q, k] / qPochhammer[q, q, k].

More precisely, qPochhammer[a, q, k] is

$$(a;q)_k=\begin{cases} (1-a)(1-aq)\dots(1-aq^{k-1}) & k>0 \\ 1 & k=0 \\ \left((1-aq^{-1})(1-aq^{-2})\dots(1-aq^{k})\right)^{-1} & k<0 \end{cases}$$

and qBinomial[n, k, q] is

$$\binom{n}{k}_q = \begin{cases} \frac {\displaystyle (q^{n-k+1};q)_k} {\displaystyle (q;q)_k } & k\geq 0 \\ 0 & k<0. \end{cases}$$

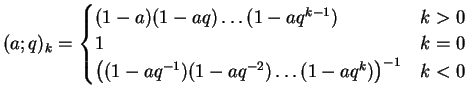
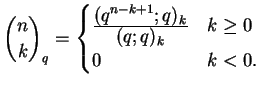
The function qExpand replaces every occurence of a qPochhammer symbol or a qBinomial symbol by its definition:

In[12]:= ?qExpand
qExpand[expr_] replaces all occurences of qPochhammer and qBinomial in expr by their definitions as products. See the documentation for qPochhammer and for qBinomial for details.

Hence,

In[13]:=	qPochhammer[a, q, 6] // qExpand
Out[13]=	2 3 4 5 (-1 + a) (-1 + a q) (-1 + a q ) (-1 + a q ) (-1 + a q ) (-1 + a q )

In[14]:=	First[s] /. {n -> 3, CJ`k[1] -> 2} // qExpand
Out[14]=	11 2 3 CJ`q (-1 + CJ`q ) (-1 + CJ`q )

Finally,

In[15]:= ?ColoredJones
Type ColoredJones and see for yourself.