 929 |
 931 |
| © | Dror Bar-Natan: The Knot Atlas: The Rolfsen Knot Table: |
|
 KnotPlot |
This page is passe. Go here
instead!
The Alternating Knot 930Visit 930's page at the Knot Server (KnotPlot driven, includes 3D interactive images!) Visit 930's page at Knotilus! |
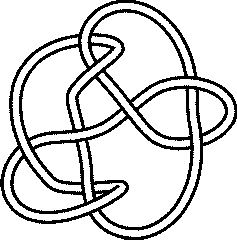 KnotPlot |
| PD Presentation: | X4251 X10,6,11,5 X8394 X2,9,3,10 X14,8,15,7 X18,15,1,16 X16,11,17,12 X12,17,13,18 X6,14,7,13 |
| Gauss Code: | {1, -4, 3, -1, 2, -9, 5, -3, 4, -2, 7, -8, 9, -5, 6, -7, 8, -6} |
| DT (Dowker-Thistlethwaite) Code: | 4 8 10 14 2 16 6 18 12 |
|
Minimum Braid Representative:
Length is 9, width is 4 Braid index is 4 |
A Morse Link Presentation:
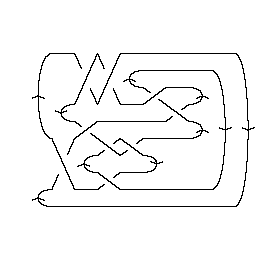
|
| 3D Invariants: |
|
| Alexander Polynomial: | - t-3 + 5t-2 - 12t-1 + 17 - 12t + 5t2 - t3 |
| Conway Polynomial: | 1 - z2 - z4 - z6 |
| Other knots with the same Alexander/Conway Polynomial: | {K11n130, ...} |
| Determinant and Signature: | {53, 0} |
| Jones Polynomial: | - q-5 + 3q-4 - 5q-3 + 8q-2 - 9q-1 + 9 - 8q + 6q2 - 3q3 + q4 |
| Other knots (up to mirrors) with the same Jones Polynomial: | {K11n114, ...} |
| A2 (sl(3)) Invariant: | - q-16 + q-12 - q-10 + 3q-8 + q-6 + q-2 - 3 + q2 - 2q4 + q6 + 2q8 - q10 + q12 |
| HOMFLY-PT Polynomial: | 2a-2 + 2a-2z2 + a-2z4 - 4 - 7z2 - 4z4 - z6 + 4a2 + 5a2z2 + 2a2z4 - a4 - a4z2 |
| Kauffman Polynomial: | - a-4z2 + a-4z4 + a-3z - 3a-3z3 + 3a-3z5 - 2a-2 + 5a-2z2 - 7a-2z4 + 5a-2z6 + a-1z - 2a-1z3 - 2a-1z5 + 4a-1z7 - 4 + 17z2 - 23z4 + 10z6 + z8 + az - 9az5 + 7az7 - 4a2 + 16a2z2 - 22a2z4 + 8a2z6 + a2z8 + 2a3z - 3a3z3 - 3a3z5 + 3a3z7 - a4 + 5a4z2 - 7a4z4 + 3a4z6 + a5z - 2a5z3 + a5z5 |
| V2 and V3, the type 2 and 3 Vassiliev invariants: | {-1, -1} |
|
Khovanov Homology:
(The squares with yellow highlighting are those on the "critical diagonals", where j-2r=s+1 or j-2r=s+1, where s=0 is the signature of 930. Nonzero entries off the critical diagonals (if any exist) are highlighted in red.) |
|
| n | Coloured Jones Polynomial (in the (n+1)-dimensional representation of sl(2)) |
| 2 | q-15 - 3q-14 + 10q-12 - 13q-11 - 6q-10 + 33q-9 - 26q-8 - 25q-7 + 64q-6 - 31q-5 - 50q-4 + 85q-3 - 25q-2 - 66q-1 + 85 - 13q - 63q2 + 63q3 - q4 - 43q5 + 31q6 + 4q7 - 18q8 + 8q9 + 2q10 - 3q11 + q12 |
| 3 | - q-30 + 3q-29 - 5q-27 - 5q-26 + 13q-25 + 13q-24 - 23q-23 - 29q-22 + 32q-21 + 59q-20 - 39q-19 - 99q-18 + 34q-17 + 152q-16 - 19q-15 - 203q-14 - 21q-13 + 262q-12 + 60q-11 - 297q-10 - 121q-9 + 332q-8 + 173q-7 - 344q-6 - 226q-5 + 347q-4 + 264q-3 - 330q-2 - 293q-1 + 302 + 306q - 260q2 - 303q3 + 209q4 + 282q5 - 151q6 - 248q7 + 97q8 + 201q9 - 49q10 - 153q11 + 21q12 + 99q13 + q14 - 61q15 - 6q16 + 32q17 + 5q18 - 14q19 - 2q20 + 4q21 + 2q22 - 3q23 + q24 |
| 4 | q-50 - 3q-49 + 5q-47 + 5q-45 - 20q-44 - 6q-43 + 23q-42 + 12q-41 + 32q-40 - 73q-39 - 53q-38 + 45q-37 + 65q-36 + 145q-35 - 153q-34 - 200q-33 - 14q-32 + 143q-31 + 445q-30 - 147q-29 - 439q-28 - 288q-27 + 105q-26 + 928q-25 + 106q-24 - 599q-23 - 783q-22 - 220q-21 + 1401q-20 + 611q-19 - 496q-18 - 1308q-17 - 810q-16 + 1652q-15 + 1180q-14 - 138q-13 - 1671q-12 - 1454q-11 + 1647q-10 + 1616q-9 + 308q-8 - 1806q-7 - 1949q-6 + 1448q-5 + 1834q-4 + 718q-3 - 1721q-2 - 2213q-1 + 1104 + 1806q + 1031q2 - 1404q3 - 2198q4 + 637q5 + 1502q6 + 1191q7 - 886q8 - 1870q9 + 164q10 + 970q11 + 1105q12 - 332q13 - 1284q14 - 133q15 + 411q16 + 779q17 + 24q18 - 661q19 - 172q20 + 55q21 + 387q22 + 112q23 - 238q24 - 82q25 - 46q26 + 129q27 + 61q28 - 61q29 - 13q30 - 28q31 + 27q32 + 16q33 - 13q34 + 2q35 - 6q36 + 4q37 + 2q38 - 3q39 + q40 |
| 5 | - q-75 + 3q-74 - 5q-72 + 2q-69 + 13q-68 + 6q-67 - 23q-66 - 21q-65 - 6q-64 + 18q-63 + 58q-62 + 45q-61 - 42q-60 - 116q-59 - 95q-58 + 26q-57 + 190q-56 + 236q-55 + 34q-54 - 294q-53 - 446q-52 - 193q-51 + 347q-50 + 746q-49 + 540q-48 - 301q-47 - 1113q-46 - 1072q-45 + 36q-44 + 1422q-43 + 1830q-42 + 543q-41 - 1593q-40 - 2692q-39 - 1485q-38 + 1429q-37 + 3600q-36 + 2735q-35 - 884q-34 - 4284q-33 - 4248q-32 - 146q-31 + 4767q-30 + 5784q-29 + 1488q-28 - 4739q-27 - 7283q-26 - 3165q-25 + 4453q-24 + 8528q-23 + 4840q-22 - 3729q-21 - 9486q-20 - 6571q-19 + 2900q-18 + 10132q-17 + 8046q-16 - 1882q-15 - 10500q-14 - 9355q-13 + 901q-12 + 10624q-11 + 10376q-10 + 93q-9 - 10548q-8 - 11181q-7 - 1006q-6 + 10252q-5 + 11735q-4 + 1923q-3 - 9757q-2 - 12056q-1 - 2802 + 9009q + 12089q2 + 3677q3 - 7986q4 - 11822q5 - 4480q6 + 6701q7 + 11178q8 + 5155q9 - 5200q10 - 10153q11 - 5597q12 + 3590q13 + 8776q14 + 5724q15 - 2033q16 - 7149q17 - 5450q18 + 663q19 + 5394q20 + 4883q21 + 325q22 - 3742q23 - 3985q24 - 936q25 + 2281q26 + 3039q27 + 1154q28 - 1232q29 - 2062q30 - 1082q31 + 500q32 + 1284q33 + 856q34 - 120q35 - 711q36 - 575q37 - 46q38 + 352q39 + 334q40 + 82q41 - 145q42 - 184q43 - 61q44 + 63q45 + 78q46 + 26q47 - 6q48 - 37q49 - 22q50 + 15q51 + 11q52 - 2q53 + 3q54 - 2q55 - 6q56 + 4q57 + 2q58 - 3q59 + q60 |
| 6 | q-105 - 3q-104 + 5q-102 - 7q-99 + 5q-98 - 13q-97 - 6q-96 + 32q-95 + 12q-94 + 6q-93 - 35q-92 - 3q-91 - 61q-90 - 37q-89 + 106q-88 + 97q-87 + 83q-86 - 78q-85 - 50q-84 - 281q-83 - 234q-82 + 189q-81 + 368q-80 + 487q-79 + 95q-78 - 27q-77 - 880q-76 - 1062q-75 - 200q-74 + 669q-73 + 1561q-72 + 1252q-71 + 917q-70 - 1544q-69 - 3022q-68 - 2336q-67 - 342q-66 + 2696q-65 + 4072q-64 + 4665q-63 - 208q-62 - 5060q-61 - 7072q-60 - 5206q-59 + 903q-58 + 6920q-57 + 12097q-56 + 6384q-55 - 3182q-54 - 12040q-53 - 14685q-52 - 7707q-51 + 4875q-50 + 19971q-49 + 18726q-48 + 6871q-47 - 11495q-46 - 24707q-45 - 23166q-44 - 6334q-43 + 21942q-42 + 32015q-41 + 24455q-40 - 1411q-39 - 28734q-38 - 39997q-37 - 25239q-36 + 14429q-35 + 39740q-34 + 43584q-33 + 16060q-32 - 23870q-31 - 51820q-30 - 45519q-29 + 65q-28 + 39502q-27 + 58150q-26 + 34702q-25 - 13004q-24 - 56500q-23 - 61480q-22 - 15434q-21 + 33915q-20 + 66234q-19 + 49597q-18 - 1056q-17 - 56063q-16 - 71459q-15 - 28185q-14 + 26675q-13 + 69304q-12 + 59637q-11 + 9292q-10 - 52952q-9 - 76599q-8 - 37814q-7 + 19152q-6 + 68839q-5 + 65948q-4 + 18458q-3 - 47408q-2 - 77764q-1 - 45553 + 10197q + 64272q2 + 68954q3 + 27760q4 - 37744q5 - 73801q6 - 51360q7 - 1437q8 + 53604q9 + 66871q10 + 36529q11 - 23006q12 - 62465q13 - 52623q14 - 14213q15 + 36348q16 + 57063q17 + 41144q18 - 5863q19 - 43764q20 - 46107q21 - 23280q22 + 16353q23 + 39809q24 + 37724q25 + 7565q26 - 22522q27 - 32162q28 - 24126q29 + 655q30 + 20456q31 + 26764q32 + 12392q33 - 6154q34 - 16308q35 - 17419q36 - 6085q37 + 6142q38 + 13916q39 + 9631q40 + 1365q41 - 5038q42 - 8702q43 - 5504q44 - 202q45 + 4970q46 + 4613q47 + 2254q48 - 298q49 - 2873q50 - 2662q51 - 1175q52 + 1143q53 + 1356q54 + 1060q55 + 505q56 - 583q57 - 805q58 - 583q59 + 183q60 + 222q61 + 255q62 + 255q63 - 60q64 - 166q65 - 165q66 + 47q67 + 10q68 + 26q69 + 68q70 - 3q71 - 24q72 - 36q73 + 21q74 - q75 - 7q76 + 14q77 - q78 - 2q79 - 6q80 + 4q81 + 2q82 - 3q83 + q84 |
| 7 | - q-140 + 3q-139 - 5q-137 + 7q-134 - 5q-132 + 13q-131 - 3q-130 - 23q-129 - 12q-128 - 6q-127 + 35q-126 + 31q-125 - 5q-124 + 42q-123 - 16q-122 - 87q-121 - 87q-120 - 86q-119 + 90q-118 + 170q-117 + 121q-116 + 202q-115 + 9q-114 - 265q-113 - 402q-112 - 538q-111 - 79q-110 + 429q-109 + 671q-108 + 1047q-107 + 598q-106 - 277q-105 - 1162q-104 - 2149q-103 - 1623q-102 - 168q-101 + 1452q-100 + 3494q-99 + 3592q-98 + 1882q-97 - 1033q-96 - 5221q-95 - 6764q-94 - 5177q-93 - 907q-92 + 6184q-91 + 10739q-90 + 10887q-89 + 5906q-88 - 5135q-87 - 14824q-86 - 18971q-85 - 14834q-84 + 106q-83 + 16730q-82 + 28303q-81 + 28515q-80 + 11200q-79 - 13917q-78 - 36794q-77 - 46006q-76 - 29803q-75 + 3154q-74 + 40523q-73 + 64964q-72 + 55884q-71 + 17916q-70 - 35776q-69 - 81246q-68 - 87023q-67 - 50124q-66 + 18811q-65 + 90197q-64 + 119293q-63 + 91670q-62 + 12099q-61 - 87038q-60 - 147372q-59 - 139368q-58 - 56314q-57 + 69551q-56 + 166245q-55 + 187209q-54 + 110653q-53 - 36434q-52 - 172069q-51 - 230685q-50 - 170584q-49 - 9038q-48 + 163756q-47 + 264303q-46 + 230046q-45 + 63812q-44 - 141581q-43 - 286634q-42 - 284915q-41 - 121869q-40 + 109569q-39 + 296342q-38 + 330748q-37 + 179153q-36 - 70743q-35 - 295693q-34 - 367093q-33 - 231134q-32 + 30306q-31 + 286912q-30 + 393037q-29 + 276036q-28 + 9110q-27 - 273437q-26 - 410688q-25 - 312837q-24 - 44562q-23 + 257631q-22 + 421529q-21 + 342270q-20 + 75535q-19 - 241544q-18 - 427749q-17 - 365409q-16 - 102197q-15 + 225747q-14 + 430664q-13 + 384105q-12 + 125684q-11 - 210137q-10 - 430936q-9 - 399497q-8 - 147605q-7 + 193300q-6 + 428330q-5 + 412620q-4 + 169564q-3 - 173788q-2 - 421788q-1 - 423183 - 192532q + 149583q2 + 409333q3 + 430356q4 + 216898q5 - 119422q6 - 389088q7 - 432054q8 - 241485q9 + 82746q10 + 358976q11 + 425772q12 + 264251q13 - 40378q14 - 318196q15 - 409021q16 - 281941q17 - 5088q18 + 267301q19 + 379836q20 + 290962q21 + 49860q22 - 208618q23 - 338081q24 - 288323q25 - 89189q26 + 146556q27 + 285618q28 + 272168q29 + 118414q30 - 86496q31 - 225975q32 - 243111q33 - 134696q34 + 34010q35 + 165116q36 + 204052q37 + 136276q38 + 6363q39 - 108154q40 - 159320q41 - 125498q42 - 32714q43 + 60818q44 + 114826q45 + 105238q46 + 44770q47 - 25322q48 - 74920q49 - 80761q50 - 45848q51 + 2667q52 + 43541q53 + 56377q54 + 39285q55 + 8931q56 - 21280q57 - 35566q58 - 29561q59 - 12632q60 + 7772q61 + 20162q62 + 19699q63 + 11553q64 - 939q65 - 9984q66 - 11668q67 - 8598q68 - 1697q69 + 4188q70 + 6200q71 + 5545q72 + 2017q73 - 1462q74 - 2855q75 - 3073q76 - 1533q77 + 234q78 + 1136q79 + 1661q80 + 938q81 - 11q82 - 416q83 - 697q84 - 439q85 - 118q86 + 57q87 + 360q88 + 256q89 + 10q90 - 41q91 - 120q92 - 48q93 - 26q94 - 43q95 + 66q96 + 54q97 - 3q98 - 11q99 - 23q100 + 7q101 + 5q102 - 19q103 + 9q104 + 10q105 - q106 - 2q107 - 6q108 + 4q109 + 2q110 - 3q111 + q112 |
Computer Talk. The data above can be recomputed by Mathematica using the package KnotTheory`. Following setup, the sample Mathematica session below reproduces most of the above data (Mathematica system prompts in blue, human input in red, Mathematica output in black):
In[1]:= |
<< KnotTheory` |
Loading KnotTheory` (version of August 30, 2005, 10:15:35)... | |
In[2]:= | PD[Knot[9, 30]] |
Out[2]= | PD[X[4, 2, 5, 1], X[10, 6, 11, 5], X[8, 3, 9, 4], X[2, 9, 3, 10], > X[14, 8, 15, 7], X[18, 15, 1, 16], X[16, 11, 17, 12], X[12, 17, 13, 18], > X[6, 14, 7, 13]] |
In[3]:= | GaussCode[Knot[9, 30]] |
Out[3]= | GaussCode[1, -4, 3, -1, 2, -9, 5, -3, 4, -2, 7, -8, 9, -5, 6, -7, 8, -6] |
In[4]:= | DTCode[Knot[9, 30]] |
Out[4]= | DTCode[4, 8, 10, 14, 2, 16, 6, 18, 12] |
In[5]:= | br = BR[Knot[9, 30]] |
Out[5]= | BR[4, {-1, -1, 2, 2, -1, 2, -3, 2, -3}] |
In[6]:= | {First[br], Crossings[br]} |
Out[6]= | {4, 9} |
In[7]:= | BraidIndex[Knot[9, 30]] |
Out[7]= | 4 |
In[8]:= | Show[DrawMorseLink[Knot[9, 30]]] |
 | |
Out[8]= | -Graphics- |
In[9]:= | #[Knot[9, 30]]& /@ {SymmetryType, UnknottingNumber, ThreeGenus, BridgeIndex, SuperBridgeIndex, NakanishiIndex} |
Out[9]= | {Reversible, 1, 3, 3, {4, 6}, 1} |
In[10]:= | alex = Alexander[Knot[9, 30]][t] |
Out[10]= | -3 5 12 2 3
17 - t + -- - -- - 12 t + 5 t - t
2 t
t |
In[11]:= | Conway[Knot[9, 30]][z] |
Out[11]= | 2 4 6 1 - z - z - z |
In[12]:= | Select[AllKnots[], (alex === Alexander[#][t])&] |
Out[12]= | {Knot[9, 30], Knot[11, NonAlternating, 130]} |
In[13]:= | {KnotDet[Knot[9, 30]], KnotSignature[Knot[9, 30]]} |
Out[13]= | {53, 0} |
In[14]:= | Jones[Knot[9, 30]][q] |
Out[14]= | -5 3 5 8 9 2 3 4
9 - q + -- - -- + -- - - - 8 q + 6 q - 3 q + q
4 3 2 q
q q q |
In[15]:= | Select[AllKnots[], (J === Jones[#][q] || (J /. q-> 1/q) === Jones[#][q])&] |
Out[15]= | {Knot[9, 30], Knot[11, NonAlternating, 114]} |
In[16]:= | A2Invariant[Knot[9, 30]][q] |
Out[16]= | -16 -12 -10 3 -6 -2 2 4 6 8 10 12
-3 - q + q - q + -- + q + q + q - 2 q + q + 2 q - q + q
8
q |
In[17]:= | HOMFLYPT[Knot[9, 30]][a, z] |
Out[17]= | 2 4
2 2 4 2 2 z 2 2 4 2 4 z 2 4 6
-4 + -- + 4 a - a - 7 z + ---- + 5 a z - a z - 4 z + -- + 2 a z - z
2 2 2
a a a |
In[18]:= | Kauffman[Knot[9, 30]][a, z] |
Out[18]= | 2 2
2 2 4 z z 3 5 2 z 5 z
-4 - -- - 4 a - a + -- + - + a z + 2 a z + a z + 17 z - -- + ---- +
2 3 a 4 2
a a a a
3 3 4 4
2 2 4 2 3 z 2 z 3 3 5 3 4 z 7 z
> 16 a z + 5 a z - ---- - ---- - 3 a z - 2 a z - 23 z + -- - ---- -
3 a 4 2
a a a
5 5
2 4 4 4 3 z 2 z 5 3 5 5 5 6
> 22 a z - 7 a z + ---- - ---- - 9 a z - 3 a z + a z + 10 z +
3 a
a
6 7
5 z 2 6 4 6 4 z 7 3 7 8 2 8
> ---- + 8 a z + 3 a z + ---- + 7 a z + 3 a z + z + a z
2 a
a |
In[19]:= | {Vassiliev[2][Knot[9, 30]], Vassiliev[3][Knot[9, 30]]} |
Out[19]= | {-1, -1} |
In[20]:= | Kh[Knot[9, 30]][q, t] |
Out[20]= | 5 1 2 1 3 2 5 3 4 5
- + 5 q + ------ + ----- + ----- + ----- + ----- + ----- + ----- + ---- + --- +
q 11 5 9 4 7 4 7 3 5 3 5 2 3 2 3 q t
q t q t q t q t q t q t q t q t
3 3 2 5 2 5 3 7 3 9 4
> 4 q t + 4 q t + 2 q t + 4 q t + q t + 2 q t + q t |
In[21]:= | ColouredJones[Knot[9, 30], 2][q] |
Out[21]= | -15 3 10 13 6 33 26 25 64 31 50 85 25
85 + q - --- + --- - --- - --- + -- - -- - -- + -- - -- - -- + -- - -- -
14 12 11 10 9 8 7 6 5 4 3 2
q q q q q q q q q q q q
66 2 3 4 5 6 7 8 9
> -- - 13 q - 63 q + 63 q - q - 43 q + 31 q + 4 q - 18 q + 8 q +
q
10 11 12
> 2 q - 3 q + q |
| Dror Bar-Natan: The Knot Atlas: The Rolfsen Knot Table: The Knot 930 |
|