© | Dror Bar-Natan: The Knot Atlas: The Rolfsen Knot Table:

1080 1082

KnotPlot

This page is passe. Go here instead!    The Alternating Knot 1081    Visit 1081's page at the Knot Server (KnotPlot driven, includes 3D interactive images!) Visit 1081's page at Knotilus! Acknowledgement

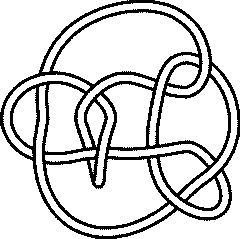KnotPlot

PD Presentation:

X4251 X8493 X12,6,13,5 X16,9,17,10 X20,17,1,18 X18,13,19,14 X14,19,15,20 X10,15,11,16 X6,12,7,11 X2837

Gauss Code:

{1, -10, 2, -1, 3, -9, 10, -2, 4, -8, 9, -3, 6, -7, 8, -4, 5, -6, 7, -5}

DT (Dowker-Thistlethwaite) Code:

4 8 12 2 16 6 18 10 20 14

Minimum Braid Representative: Length is 12, width is 5 Braid index is 5

A Morse Link Presentation:

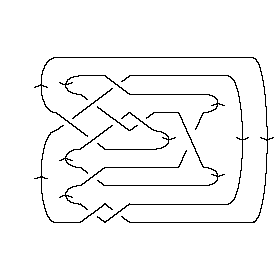
3D Invariants:

Symmetry Type Unknotting Number 3-Genus Bridge/Super Bridge Index Nakanishi Index NegativeAmphicheiral 2 3 3 / NotAvailable 1

Alexander Polynomial:

- t-3 + 8t-2 - 20t-1 + 27 - 20t + 8t2 - t3

Conway Polynomial:

1 + 3z2 + 2z4 - z6

Other knots with the same Alexander/Conway Polynomial:

{...}

Determinant and Signature:

{85, 0}

Jones Polynomial:

- q-5 + 3q-4 - 7q-3 + 11q-2 - 13q-1 + 15 - 13q + 11q2 - 7q3 + 3q4 - q5

Other knots (up to mirrors) with the same Jones Polynomial:

{10109, ...}

A2 (sl(3)) Invariant:

- q-16 + q-12 - 3q-10 + 2q-8 - q-4 + 4q-2 - 1 + 4q2 - q4 + 2q8 - 3q10 + q12 - q16

HOMFLY-PT Polynomial:

- a-4 - a-4z2 + a-2 + 3a-2z2 + 2a-2z4 + 1 - z2 - 2z4 - z6 + a2 + 3a2z2 + 2a2z4 - a4 - a4z2

Kauffman Polynomial:

a-5z - 2a-5z3 + a-5z5 - a-4 + 3a-4z2 - 5a-4z4 + 3a-4z6 - 2a-3z + 5a-3z3 - 8a-3z5 + 5a-3z7 - a-2 + 6a-2z2 - 9a-2z4 + 4a-2z8 - 8a-1z + 25a-1z3 - 31a-1z5 + 13a-1z7 + a-1z9 + 1 + 6z2 - 8z4 - 6z6 + 8z8 - 8az + 25az3 - 31az5 + 13az7 + az9 - a2 + 6a2z2 - 9a2z4 + 4a2z8 - 2a3z + 5a3z3 - 8a3z5 + 5a3z7 - a4 + 3a4z2 - 5a4z4 + 3a4z6 + a5z - 2a5z3 + a5z5

V2 and V3, the type 2 and 3 Vassiliev invariants:

{3, 0}

Khovanov Homology: (The squares with yellow highlighting are those on the "critical diagonals", where j-2r=s+1 or j-2r=s+1, where s=0 is the signature of 1081. Nonzero entries off the critical diagonals (if any exist) are highlighted in red.)

trqj r = -5 r = -4 r = -3 r = -2 r = -1 r = 0 r = 1 r = 2 r = 3 r = 4 r = 5 j = 11                     1 j = 9                   2   j = 7                 5 1   j = 5               6 2     j = 3             7 5       j = 1           8 6         j = -1         6 8           j = -3       5 7             j = -5     2 6               j = -7   1 5                 j = -9   2                   j = -11 1

n	Coloured Jones Polynomial (in the (n+1)-dimensional representation of sl(2))
2	q-15 - 3q-14 + 2q-13 + 9q-12 - 21q-11 + 4q-10 + 43q-9 - 60q-8 - 10q-7 + 108q-6 - 98q-5 - 48q-4 + 172q-3 - 109q-2 - 89q-1 + 199 - 89q - 109q2 + 172q3 - 48q4 - 98q5 + 108q6 - 10q7 - 60q8 + 43q9 + 4q10 - 21q11 + 9q12 + 2q13 - 3q14 + q15
3	- q-30 + 3q-29 - 2q-28 - 4q-27 + q-26 + 17q-25 - 5q-24 - 39q-23 + 2q-22 + 83q-21 + 12q-20 - 144q-19 - 64q-18 + 237q-17 + 144q-16 - 320q-15 - 287q-14 + 395q-13 + 472q-12 - 440q-11 - 677q-10 + 430q-9 + 894q-8 - 387q-7 - 1074q-6 + 290q-5 + 1235q-4 - 196q-3 - 1308q-2 + 54q-1 + 1359 + 54q - 1308q2 - 196q3 + 1235q4 + 290q5 - 1074q6 - 387q7 + 894q8 + 430q9 - 677q10 - 440q11 + 472q12 + 395q13 - 287q14 - 320q15 + 144q16 + 237q17 - 64q18 - 144q19 + 12q20 + 83q21 + 2q22 - 39q23 - 5q24 + 17q25 + q26 - 4q27 - 2q28 + 3q29 - q30
4	q-50 - 3q-49 + 2q-48 + 4q-47 - 6q-46 + 3q-45 - 16q-44 + 16q-43 + 34q-42 - 29q-41 - 14q-40 - 87q-39 + 62q-38 + 185q-37 - 25q-36 - 96q-35 - 399q-34 + 58q-33 + 615q-32 + 278q-31 - 116q-30 - 1255q-29 - 429q-28 + 1230q-27 + 1314q-26 + 525q-25 - 2569q-24 - 1990q-23 + 1284q-22 + 3006q-21 + 2539q-20 - 3483q-19 - 4520q-18 - 33q-17 + 4439q-16 + 5724q-15 - 3114q-14 - 6965q-13 - 2568q-12 + 4730q-11 + 8927q-10 - 1545q-9 - 8332q-8 - 5289q-7 + 3864q-6 + 11073q-5 + 460q-4 - 8389q-3 - 7331q-2 + 2332q-1 + 11797 + 2332q - 7331q2 - 8389q3 + 460q4 + 11073q5 + 3864q6 - 5289q7 - 8332q8 - 1545q9 + 8927q10 + 4730q11 - 2568q12 - 6965q13 - 3114q14 + 5724q15 + 4439q16 - 33q17 - 4520q18 - 3483q19 + 2539q20 + 3006q21 + 1284q22 - 1990q23 - 2569q24 + 525q25 + 1314q26 + 1230q27 - 429q28 - 1255q29 - 116q30 + 278q31 + 615q32 + 58q33 - 399q34 - 96q35 - 25q36 + 185q37 + 62q38 - 87q39 - 14q40 - 29q41 + 34q42 + 16q43 - 16q44 + 3q45 - 6q46 + 4q47 + 2q48 - 3q49 + q50
5	- q-75 + 3q-74 - 2q-73 - 4q-72 + 6q-71 + 2q-70 - 4q-69 + 5q-68 - 11q-67 - 22q-66 + 23q-65 + 43q-64 + 11q-63 - 14q-62 - 90q-61 - 112q-60 + 40q-59 + 238q-58 + 245q-57 + 2q-56 - 416q-55 - 645q-54 - 200q-53 + 710q-52 + 1312q-51 + 783q-50 - 897q-49 - 2429q-48 - 2020q-47 + 699q-46 + 3831q-45 + 4318q-44 + 432q-43 - 5363q-42 - 7663q-41 - 3090q-40 + 6098q-39 + 12133q-38 + 7872q-37 - 5472q-36 - 16917q-35 - 14774q-34 + 2252q-33 + 21133q-32 + 23676q-31 + 3836q-30 - 23638q-29 - 33459q-28 - 12909q-27 + 23384q-26 + 43029q-25 + 24403q-24 - 20125q-23 - 51135q-22 - 36996q-21 + 13867q-20 + 56767q-19 + 49718q-18 - 5493q-17 - 59785q-16 - 60976q-15 - 4204q-14 + 60057q-13 + 70514q-12 + 13932q-11 - 58298q-10 - 77413q-9 - 23291q-8 + 54796q-7 + 82432q-6 + 31414q-5 - 50368q-4 - 84899q-3 - 38762q-2 + 44856q-1 + 86051 + 44856q - 38762q2 - 84899q3 - 50368q4 + 31414q5 + 82432q6 + 54796q7 - 23291q8 - 77413q9 - 58298q10 + 13932q11 + 70514q12 + 60057q13 - 4204q14 - 60976q15 - 59785q16 - 5493q17 + 49718q18 + 56767q19 + 13867q20 - 36996q21 - 51135q22 - 20125q23 + 24403q24 + 43029q25 + 23384q26 - 12909q27 - 33459q28 - 23638q29 + 3836q30 + 23676q31 + 21133q32 + 2252q33 - 14774q34 - 16917q35 - 5472q36 + 7872q37 + 12133q38 + 6098q39 - 3090q40 - 7663q41 - 5363q42 + 432q43 + 4318q44 + 3831q45 + 699q46 - 2020q47 - 2429q48 - 897q49 + 783q50 + 1312q51 + 710q52 - 200q53 - 645q54 - 416q55 + 2q56 + 245q57 + 238q58 + 40q59 - 112q60 - 90q61 - 14q62 + 11q63 + 43q64 + 23q65 - 22q66 - 11q67 + 5q68 - 4q69 + 2q70 + 6q71 - 4q72 - 2q73 + 3q74 - q75

Computer Talk. The data above can be recomputed by Mathematica using the package KnotTheory`. Following setup, the sample Mathematica session below reproduces most of the above data (Mathematica system prompts in blue, human input in red, Mathematica output in black):

In[1]:=	<< KnotTheory`
Loading KnotTheory` (version of August 30, 2005, 10:15:35)...
In[2]:=	PD[Knot[10, 81]]
Out[2]=	PD[X[4, 2, 5, 1], X[8, 4, 9, 3], X[12, 6, 13, 5], X[16, 9, 17, 10], > X[20, 17, 1, 18], X[18, 13, 19, 14], X[14, 19, 15, 20], X[10, 15, 11, 16], > X[6, 12, 7, 11], X[2, 8, 3, 7]]
In[3]:=	GaussCode[Knot[10, 81]]
Out[3]=	GaussCode[1, -10, 2, -1, 3, -9, 10, -2, 4, -8, 9, -3, 6, -7, 8, -4, 5, -6, 7, > -5]
In[4]:=	DTCode[Knot[10, 81]]
Out[4]=	DTCode[4, 8, 12, 2, 16, 6, 18, 10, 20, 14]
In[5]:=	br = BR[Knot[10, 81]]
Out[5]=	BR[5, {1, 1, -2, 1, 3, 2, 2, -4, -3, -3, -3, -4}]
In[6]:=	{First[br], Crossings[br]}
Out[6]=	{5, 12}
In[7]:=	BraidIndex[Knot[10, 81]]
Out[7]=	5
In[8]:=	Show[DrawMorseLink[Knot[10, 81]]]
Out[8]=	-Graphics-
In[9]:=	#[Knot[10, 81]]& /@ {SymmetryType, UnknottingNumber, ThreeGenus, BridgeIndex, SuperBridgeIndex, NakanishiIndex}
Out[9]=	{NegativeAmphicheiral, 2, 3, 3, NotAvailable, 1}
In[10]:=	alex = Alexander[Knot[10, 81]][t]
Out[10]=	-3 8 20 2 3 27 - t + -- - -- - 20 t + 8 t - t 2 t t
In[11]:=	Conway[Knot[10, 81]][z]
Out[11]=	2 4 6 1 + 3 z + 2 z - z
In[12]:=	Select[AllKnots[], (alex === Alexander[#][t])&]
Out[12]=	{Knot[10, 81]}
In[13]:=	{KnotDet[Knot[10, 81]], KnotSignature[Knot[10, 81]]}
Out[13]=	{85, 0}
In[14]:=	Jones[Knot[10, 81]][q]
Out[14]=	-5 3 7 11 13 2 3 4 5 15 - q + -- - -- + -- - -- - 13 q + 11 q - 7 q + 3 q - q 4 3 2 q q q q
In[15]:=	Select[AllKnots[], (J === Jones[#][q] || (J /. q-> 1/q) === Jones[#][q])&]
Out[15]=	{Knot[10, 81], Knot[10, 109]}
In[16]:=	A2Invariant[Knot[10, 81]][q]
Out[16]=	-16 -12 3 2 -4 4 2 4 8 10 12 16 -1 - q + q - --- + -- - q + -- + 4 q - q + 2 q - 3 q + q - q 10 8 2 q q q
In[17]:=	HOMFLYPT[Knot[10, 81]][a, z]
Out[17]=	2 2 4 -4 -2 2 4 2 z 3 z 2 2 4 2 4 2 z 1 - a + a + a - a - z - -- + ---- + 3 a z - a z - 2 z + ---- + 4 2 2 a a a 2 4 6 > 2 a z - z
In[18]:=	Kauffman[Knot[10, 81]][a, z]
Out[18]=	-4 -2 2 4 z 2 z 8 z 3 5 2 1 - a - a - a - a + -- - --- - --- - 8 a z - 2 a z + a z + 6 z + 5 3 a a a 2 2 3 3 3 3 z 6 z 2 2 4 2 2 z 5 z 25 z 3 3 3 > ---- + ---- + 6 a z + 3 a z - ---- + ---- + ----- + 25 a z + 5 a z - 4 2 5 3 a a a a a 4 4 5 5 5 5 3 4 5 z 9 z 2 4 4 4 z 8 z 31 z > 2 a z - 8 z - ---- - ---- - 9 a z - 5 a z + -- - ---- - ----- - 4 2 5 3 a a a a a 6 7 7 5 3 5 5 5 6 3 z 4 6 5 z 13 z > 31 a z - 8 a z + a z - 6 z + ---- + 3 a z + ---- + ----- + 4 3 a a a 8 9 7 3 7 8 4 z 2 8 z 9 > 13 a z + 5 a z + 8 z + ---- + 4 a z + -- + a z 2 a a
In[19]:=	{Vassiliev[2][Knot[10, 81]], Vassiliev[3][Knot[10, 81]]}
Out[19]=	{3, 0}
In[20]:=	Kh[Knot[10, 81]][q, t]
Out[20]=	8 1 2 1 5 2 6 5 7 6 - + 8 q + ------ + ----- + ----- + ----- + ----- + ----- + ----- + ---- + --- + q 11 5 9 4 7 4 7 3 5 3 5 2 3 2 3 q t q t q t q t q t q t q t q t q t 3 3 2 5 2 5 3 7 3 7 4 9 4 > 6 q t + 7 q t + 5 q t + 6 q t + 2 q t + 5 q t + q t + 2 q t + 11 5 > q t
In[21]:=	ColouredJones[Knot[10, 81], 2][q]
Out[21]=	-15 3 2 9 21 4 43 60 10 108 98 48 172 199 + q - --- + --- + --- - --- + --- + -- - -- - -- + --- - -- - -- + --- - 14 13 12 11 10 9 8 7 6 5 4 3 q q q q q q q q q q q q 109 89 2 3 4 5 6 7 > --- - -- - 89 q - 109 q + 172 q - 48 q - 98 q + 108 q - 10 q - 2 q q 8 9 10 11 12 13 14 15 > 60 q + 43 q + 4 q - 21 q + 9 q + 2 q - 3 q + q

Dror Bar-Natan: The Knot Atlas: The Rolfsen Knot Table: The Knot 1081

1080 1082