 10157 |
 10159 |
| © | Dror Bar-Natan: The Knot Atlas: The Rolfsen Knot Table: |
|
 KnotPlot |
This page is passe. Go here
instead!
The Non Alternating Knot 10158Visit 10158's page at the Knot Server (KnotPlot driven, includes 3D interactive images!) Visit 10158's page at Knotilus! |
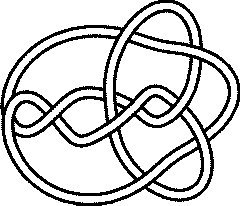 KnotPlot |
| PD Presentation: | X6271 X3,10,4,11 X14,8,15,7 X8,14,9,13 X9,2,10,3 X11,18,12,19 X5,17,6,16 X17,5,18,4 X20,16,1,15 X19,12,20,13 |
| Gauss Code: | {1, 5, -2, 8, -7, -1, 3, -4, -5, 2, -6, 10, 4, -3, 9, 7, -8, 6, -10, -9} |
| DT (Dowker-Thistlethwaite) Code: | 6 -10 -16 14 -2 -18 8 20 -4 -12 |
|
Minimum Braid Representative:
Length is 11, width is 4 Braid index is 4 |
A Morse Link Presentation:
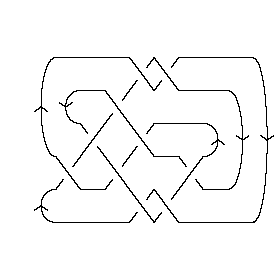
|
| 3D Invariants: |
|
| Alexander Polynomial: | - t-3 + 4t-2 - 10t-1 + 15 - 10t + 4t2 - t3 |
| Conway Polynomial: | 1 - 3z2 - 2z4 - z6 |
| Other knots with the same Alexander/Conway Polynomial: | {...} |
| Determinant and Signature: | {45, 0} |
| Jones Polynomial: | q-4 - 3q-3 + 6q-2 - 7q-1 + 8 - 8q + 6q2 - 4q3 + 2q4 |
| Other knots (up to mirrors) with the same Jones Polynomial: | {...} |
| A2 (sl(3)) Invariant: | q-12 - q-10 + 2q-8 + q-6 - q-4 + 2q-2 - 2 + q2 - 2q4 - q6 + q8 - q10 + 2q12 + q14 |
| HOMFLY-PT Polynomial: | a-4 + a-2z2 + a-2z4 - 2 - 6z2 - 4z4 - z6 + 2a2 + 2a2z2 + a2z4 |
| Kauffman Polynomial: | a-4 - 5a-4z2 + 3a-4z4 + 2a-3z - 4a-3z3 + a-3z5 + a-3z7 - 2a-2z2 - a-2z4 + a-2z6 + a-2z8 + a-1z + 2a-1z3 - 7a-1z5 + 5a-1z7 - 2 + 9z2 - 13z4 + 6z6 + z8 - az + 3az3 - 5az5 + 4az7 - 2a2 + 5a2z2 - 8a2z4 + 5a2z6 - 3a3z3 + 3a3z5 - a4z2 + a4z4 |
| V2 and V3, the type 2 and 3 Vassiliev invariants: | {-3, -1} |
|
Khovanov Homology:
(The squares with yellow highlighting are those on the "critical diagonals", where j-2r=s+1 or j-2r=s+1, where s=0 is the signature of 10158. Nonzero entries off the critical diagonals (if any exist) are highlighted in red.) |
|
| n | Coloured Jones Polynomial (in the (n+1)-dimensional representation of sl(2)) |
| 2 | q-12 - 3q-11 + 2q-10 + 8q-9 - 17q-8 + 2q-7 + 31q-6 - 36q-5 - 9q-4 + 58q-3 - 46q-2 - 24q-1 + 73 - 42q - 33q2 + 67q3 - 26q4 - 33q5 + 44q6 - 7q7 - 23q8 + 17q9 + 2q10 - 8q11 + 2q12 + q13 |
| 3 | q-24 - 3q-23 + 2q-22 + 4q-21 - 2q-20 - 13q-19 + 3q-18 + 31q-17 - 58q-15 - 14q-14 + 88q-13 + 52q-12 - 128q-11 - 95q-10 + 148q-9 + 159q-8 - 164q-7 - 216q-6 + 158q-5 + 274q-4 - 149q-3 - 309q-2 + 125q-1 + 334 - 98q - 341q2 + 67q3 + 331q4 - 29q5 - 312q6 - 4q7 + 271q8 + 44q9 - 226q10 - 71q11 + 170q12 + 84q13 - 110q14 - 85q15 + 61q16 + 69q17 - 22q18 - 48q19 + 4q20 + 22q21 + 8q22 - 12q23 - 2q24 + 2q26 |
| 4 | q-40 - 3q-39 + 2q-38 + 4q-37 - 6q-36 + 2q-35 - 12q-34 + 14q-33 + 26q-32 - 23q-31 - 11q-30 - 64q-29 + 41q-28 + 127q-27 - 2q-26 - 53q-25 - 263q-24 - q-23 + 338q-22 + 211q-21 + 10q-20 - 658q-19 - 318q-18 + 491q-17 + 666q-16 + 389q-15 - 1030q-14 - 911q-13 + 341q-12 + 1112q-11 + 1039q-10 - 1121q-9 - 1485q-8 - 65q-7 + 1300q-6 + 1639q-5 - 951q-4 - 1785q-3 - 482q-2 + 1232q-1 + 1980 - 679q - 1803q2 - 781q3 + 1007q4 + 2060q5 - 352q6 - 1608q7 - 993q8 + 652q9 + 1927q10 + 39q11 - 1211q12 - 1101q13 + 177q14 + 1549q15 + 406q16 - 635q17 - 995q18 - 274q19 + 948q20 + 542q21 - 75q22 - 626q23 - 455q24 + 337q25 + 369q26 + 199q27 - 201q28 - 315q29 + 2q30 + 105q31 + 156q32 + 13q33 - 97q34 - 41q35 - 11q36 + 39q37 + 23q38 - 6q39 - 6q40 - 8q41 + 2q43 + q44 |
| 5 | q-60 - 3q-59 + 2q-58 + 4q-57 - 6q-56 - 2q-55 + 3q-54 - q-53 + 9q-52 + 14q-51 - 17q-50 - 36q-49 - 10q-48 + 18q-47 + 68q-46 + 75q-45 - 18q-44 - 159q-43 - 189q-42 - 25q-41 + 252q-40 + 429q-39 + 213q-38 - 337q-37 - 805q-36 - 636q-35 + 290q-34 + 1281q-33 + 1350q-32 + 80q-31 - 1710q-30 - 2419q-29 - 890q-28 + 1971q-27 + 3616q-26 + 2186q-25 - 1719q-24 - 4867q-23 - 3918q-22 + 1034q-21 + 5805q-20 + 5791q-19 + 259q-18 - 6351q-17 - 7664q-16 - 1780q-15 + 6359q-14 + 9194q-13 + 3490q-12 - 5983q-11 - 10328q-10 - 5021q-9 + 5295q-8 + 10977q-7 + 6352q-6 - 4511q-5 - 11259q-4 - 7312q-3 + 3678q-2 + 11225q-1 + 8024 - 2896q - 10991q2 - 8488q3 + 2135q4 + 10574q5 + 8795q6 - 1322q7 - 9999q8 - 9020q9 + 468q10 + 9223q11 + 9079q12 + 547q13 - 8176q14 - 9057q15 - 1604q16 + 6878q17 + 8717q18 + 2711q19 - 5279q20 - 8103q21 - 3682q22 + 3532q23 + 7080q24 + 4346q25 - 1729q26 - 5714q27 - 4574q28 + 114q29 + 4125q30 + 4293q31 + 1081q32 - 2475q33 - 3571q34 - 1760q35 + 1060q36 + 2563q37 + 1879q38 - 20q39 - 1535q40 - 1585q41 - 502q42 + 644q43 + 1082q44 + 663q45 - 124q46 - 580q47 - 495q48 - 151q49 + 199q50 + 327q51 + 157q52 - 32q53 - 110q54 - 112q55 - 44q56 + 40q57 + 46q58 + 18q59 + 10q60 - 12q61 - 12q62 - 4q63 + 2q64 + 2q66 |
| 6 | q-84 - 3q-83 + 2q-82 + 4q-81 - 6q-80 - 2q-79 - q-78 + 14q-77 - 6q-76 - 3q-75 + 20q-74 - 31q-73 - 23q-72 - 8q-71 + 59q-70 + 28q-69 + 14q-68 + 59q-67 - 125q-66 - 165q-65 - 124q-64 + 155q-63 + 217q-62 + 290q-61 + 371q-60 - 283q-59 - 729q-58 - 934q-57 - 182q-56 + 510q-55 + 1423q-54 + 2083q-53 + 529q-52 - 1529q-51 - 3501q-50 - 2934q-49 - 1027q-48 + 2925q-47 + 6757q-46 + 5509q-45 + 603q-44 - 6722q-43 - 10062q-42 - 8917q-41 + 65q-40 + 12231q-39 + 16738q-38 + 11338q-37 - 4160q-36 - 18027q-35 - 24716q-34 - 13435q-33 + 10489q-32 + 28894q-31 + 31009q-30 + 10460q-29 - 17708q-28 - 41141q-27 - 36090q-26 - 3966q-25 + 32154q-24 + 50518q-23 + 33670q-22 - 4933q-21 - 48179q-20 - 57448q-19 - 25874q-18 + 23623q-17 + 60275q-16 + 54540q-15 + 13888q-14 - 44099q-13 - 68900q-12 - 44730q-11 + 9892q-10 + 59592q-9 + 66002q-8 + 29559q-7 - 35066q-6 - 70716q-5 - 55314q-4 - 1702q-3 + 53985q-2 + 69206q-1 + 38770 - 26585q - 67754q2 - 59520q3 - 9520q4 + 47482q5 + 68412q6 + 43936q7 - 19072q8 - 62882q9 - 61087q10 - 16293q11 + 39708q12 + 65607q13 + 48293q14 - 9724q15 - 55134q16 - 61232q17 - 24708q18 + 27904q19 + 59237q20 + 52198q21 + 3463q22 - 41701q23 - 57558q24 - 33987q25 + 10739q26 + 46125q27 + 52054q28 + 18315q29 - 21794q30 - 46125q31 - 38908q32 - 8209q33 + 25729q34 + 42963q35 + 27898q36 - 281q37 - 26563q38 - 33606q39 - 20582q40 + 4011q41 + 24981q42 + 25817q43 + 13461q44 - 5949q45 - 18853q46 - 20164q47 - 9153q48 + 6345q49 + 14064q50 + 14062q51 + 5739q52 - 3860q53 - 10545q54 - 9745q55 - 3377q56 + 2524q57 + 6668q58 + 6130q59 + 2869q60 - 1793q61 - 4097q62 - 3549q63 - 1827q64 + 724q65 + 2127q66 + 2323q67 + 958q68 - 286q69 - 961q70 - 1148q71 - 624q72 - 12q73 + 520q74 + 462q75 + 294q76 + 72q77 - 151q78 - 201q79 - 149q80 - 13q81 + 27q82 + 53q83 + 49q84 + 23q85 - 6q86 - 16q87 - 8q88 - 6q89 + 2q92 + q93 |
Computer Talk. The data above can be recomputed by Mathematica using the package KnotTheory`. Following setup, the sample Mathematica session below reproduces most of the above data (Mathematica system prompts in blue, human input in red, Mathematica output in black):
In[1]:= |
<< KnotTheory` |
Loading KnotTheory` (version of August 30, 2005, 10:15:35)... | |
In[2]:= | PD[Knot[10, 158]] |
Out[2]= | PD[X[6, 2, 7, 1], X[3, 10, 4, 11], X[14, 8, 15, 7], X[8, 14, 9, 13], > X[9, 2, 10, 3], X[11, 18, 12, 19], X[5, 17, 6, 16], X[17, 5, 18, 4], > X[20, 16, 1, 15], X[19, 12, 20, 13]] |
In[3]:= | GaussCode[Knot[10, 158]] |
Out[3]= | GaussCode[1, 5, -2, 8, -7, -1, 3, -4, -5, 2, -6, 10, 4, -3, 9, 7, -8, 6, -10, > -9] |
In[4]:= | DTCode[Knot[10, 158]] |
Out[4]= | DTCode[6, -10, -16, 14, -2, -18, 8, 20, -4, -12] |
In[5]:= | br = BR[Knot[10, 158]] |
Out[5]= | BR[4, {-1, -1, -1, -2, 1, 1, 3, 2, -1, 2, 3}] |
In[6]:= | {First[br], Crossings[br]} |
Out[6]= | {4, 11} |
In[7]:= | BraidIndex[Knot[10, 158]] |
Out[7]= | 4 |
In[8]:= | Show[DrawMorseLink[Knot[10, 158]]] |
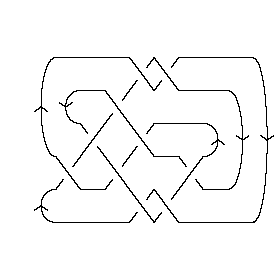 | |
Out[8]= | -Graphics- |
In[9]:= | #[Knot[10, 158]]& /@ {SymmetryType, UnknottingNumber, ThreeGenus, BridgeIndex, SuperBridgeIndex, NakanishiIndex} |
Out[9]= | {Reversible, 2, 3, 3, NotAvailable, 1} |
In[10]:= | alex = Alexander[Knot[10, 158]][t] |
Out[10]= | -3 4 10 2 3
15 - t + -- - -- - 10 t + 4 t - t
2 t
t |
In[11]:= | Conway[Knot[10, 158]][z] |
Out[11]= | 2 4 6 1 - 3 z - 2 z - z |
In[12]:= | Select[AllKnots[], (alex === Alexander[#][t])&] |
Out[12]= | {Knot[10, 158]} |
In[13]:= | {KnotDet[Knot[10, 158]], KnotSignature[Knot[10, 158]]} |
Out[13]= | {45, 0} |
In[14]:= | Jones[Knot[10, 158]][q] |
Out[14]= | -4 3 6 7 2 3 4
8 + q - -- + -- - - - 8 q + 6 q - 4 q + 2 q
3 2 q
q q |
In[15]:= | Select[AllKnots[], (J === Jones[#][q] || (J /. q-> 1/q) === Jones[#][q])&] |
Out[15]= | {Knot[10, 158]} |
In[16]:= | A2Invariant[Knot[10, 158]][q] |
Out[16]= | -12 -10 2 -6 -4 2 2 4 6 8 10 12 14
-2 + q - q + -- + q - q + -- + q - 2 q - q + q - q + 2 q + q
8 2
q q |
In[17]:= | HOMFLYPT[Knot[10, 158]][a, z] |
Out[17]= | 2 4
-4 2 2 z 2 2 4 z 2 4 6
-2 + a + 2 a - 6 z + -- + 2 a z - 4 z + -- + a z - z
2 2
a a |
In[18]:= | Kauffman[Knot[10, 158]][a, z] |
Out[18]= | 2 2 3
-4 2 2 z z 2 5 z 2 z 2 2 4 2 4 z
-2 + a - 2 a + --- + - - a z + 9 z - ---- - ---- + 5 a z - a z - ---- +
3 a 4 2 3
a a a a
3 4 4 5 5
2 z 3 3 3 4 3 z z 2 4 4 4 z 7 z
> ---- + 3 a z - 3 a z - 13 z + ---- - -- - 8 a z + a z + -- - ---- -
a 4 2 3 a
a a a
6 7 7 8
5 3 5 6 z 2 6 z 5 z 7 8 z
> 5 a z + 3 a z + 6 z + -- + 5 a z + -- + ---- + 4 a z + z + --
2 3 a 2
a a a |
In[19]:= | {Vassiliev[2][Knot[10, 158]], Vassiliev[3][Knot[10, 158]]} |
Out[19]= | {-3, -1} |
In[20]:= | Kh[Knot[10, 158]][q, t] |
Out[20]= | 5 1 2 1 4 2 3 4 3
- + 4 q + ----- + ----- + ----- + ----- + ----- + ---- + --- + 4 q t + 4 q t +
q 9 4 7 3 5 3 5 2 3 2 3 q t
q t q t q t q t q t q t
3 2 5 2 5 3 7 3 9 4
> 2 q t + 4 q t + 2 q t + 2 q t + 2 q t |
In[21]:= | ColouredJones[Knot[10, 158], 2][q] |
Out[21]= | -12 3 2 8 17 2 31 36 9 58 46 24
73 + q - --- + --- + -- - -- + -- + -- - -- - -- + -- - -- - -- - 42 q -
11 10 9 8 7 6 5 4 3 2 q
q q q q q q q q q q
2 3 4 5 6 7 8 9 10
> 33 q + 67 q - 26 q - 33 q + 44 q - 7 q - 23 q + 17 q + 2 q -
11 12 13
> 8 q + 2 q + q |
| Dror Bar-Natan: The Knot Atlas: The Rolfsen Knot Table: The Knot 10158 |
|