 10160 |
 10162 |
| © | Dror Bar-Natan: The Knot Atlas: The Rolfsen Knot Table: |
|
 KnotPlot |
This page is passe. Go here
instead!
The Non Alternating Knot 10161Visit 10161's page at the Knot Server (KnotPlot driven, includes 3D interactive images!) Visit 10161's page at Knotilus! |
 KnotPlot |
Warning. In 1974 K. Perko noticed that the knots labeled 10161 and 10162 in Rolfsen's tables are in fact the same. In our table we removed his 10162 and renumbered the subsequent knots, so that our 10 crossings total is 165, one less than Rolfsen's 166. Read more: 1 2 3 4.
| PD Presentation: | X1425 X3,12,4,13 X7,14,8,15 X18,9,19,10 X6,19,7,20 X16,5,17,6 X10,17,11,18 X13,8,14,9 X20,15,1,16 X11,2,12,3 |
| Gauss Code: | {-1, 10, -2, 1, 6, -5, -3, 8, 4, -7, -10, 2, -8, 3, 9, -6, 7, -4, 5, -9} |
| DT (Dowker-Thistlethwaite) Code: | 4 12 -16 14 -18 2 8 -20 -10 -6 |
|
Minimum Braid Representative:
Length is 10, width is 3 Braid index is 3 |
A Morse Link Presentation:
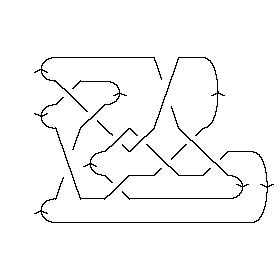
|
| 3D Invariants: |
|
| Alexander Polynomial: | t-3 - 2t-1 + 3 - 2t + t3 |
| Conway Polynomial: | 1 + 7z2 + 6z4 + z6 |
| Other knots with the same Alexander/Conway Polynomial: | {...} |
| Determinant and Signature: | {5, -4} |
| Jones Polynomial: | - q-11 + q-10 - q-9 + q-8 - q-7 + q-6 + q-3 |
| Other knots (up to mirrors) with the same Jones Polynomial: | {...} |
| A2 (sl(3)) Invariant: | - q-34 - q-30 - q-28 + q-22 + q-18 + q-16 + q-14 + q-12 + q-10 |
| HOMFLY-PT Polynomial: | 3a6 + 9a6z2 + 6a6z4 + a6z6 - a8 - a8z2 - a10 - a10z2 |
| Kauffman Polynomial: | - 3a6 + 9a6z2 - 6a6z4 + a6z6 + 2a7z - a7z3 - a8 + 3a8z2 - a8z4 + a10 - 3a10z2 + a10z4 + a11z - 3a11z3 + a11z5 + 3a12z2 - 4a12z4 + a12z6 + 3a13z - 4a13z3 + a13z5 |
| V2 and V3, the type 2 and 3 Vassiliev invariants: | {7, -18} |
|
Khovanov Homology:
(The squares with yellow highlighting are those on the "critical diagonals", where j-2r=s+1 or j-2r=s+1, where s=-4 is the signature of 10161. Nonzero entries off the critical diagonals (if any exist) are highlighted in red.) |
|
| n | Coloured Jones Polynomial (in the (n+1)-dimensional representation of sl(2)) |
| 2 | q-31 - q-30 - q-29 + 2q-28 - 2q-26 + q-25 + q-24 - q-23 - q-22 + q-21 - 2q-19 + 2q-18 - 2q-16 + q-15 + q-14 - q-13 + q-11 + q-6 |
| 3 | - q-60 + q-59 + q-58 - 2q-56 - q-55 + 2q-54 + 2q-53 - q-52 - 2q-51 + q-49 + q-47 - 2q-45 - q-44 + 4q-43 + 2q-42 - 5q-41 - 2q-40 + 6q-39 + 2q-38 - 7q-37 - 2q-36 + 6q-35 + 2q-34 - 7q-33 - 2q-32 + 6q-31 + 3q-30 - 6q-29 - 3q-28 + 4q-27 + 4q-26 - 2q-25 - 4q-24 + 3q-22 - 2q-19 + q-18 + q-16 + q-9 |
| 4 | q-98 - q-97 - q-96 + 3q-93 - q-91 - 2q-90 - 3q-89 + 3q-88 + 2q-87 + q-86 - 2q-84 - q-82 - 2q-81 + q-80 + 4q-79 + 3q-78 - q-77 - 9q-76 - 5q-75 + 7q-74 + 10q-73 + 4q-72 - 12q-71 - 11q-70 + 4q-69 + 13q-68 + 10q-67 - 12q-66 - 15q-65 + q-64 + 15q-63 + 13q-62 - 12q-61 - 17q-60 + q-59 + 15q-58 + 14q-57 - 13q-56 - 18q-55 + 2q-54 + 15q-53 + 14q-52 - 12q-51 - 18q-50 + 14q-48 + 13q-47 - 8q-46 - 15q-45 - 3q-44 + 8q-43 + 9q-42 - 7q-40 - 4q-39 + q-38 + 2q-37 + 3q-36 - q-35 + q-34 - 3q-32 - q-30 + 2q-29 + 2q-28 - q-27 - 2q-25 + q-23 + q-21 + q-12 |
| 5 | - q-145 + q-144 + q-143 - q-140 - 2q-139 - q-138 + 2q-137 + 2q-136 + 2q-135 + q-134 - 2q-133 - 4q-132 - 2q-131 + q-130 + q-129 + 2q-128 + 2q-127 + q-126 + q-124 - 3q-123 - 6q-122 - 3q-121 + q-120 + 7q-119 + 10q-118 + 5q-117 - 7q-116 - 14q-115 - 12q-114 + 2q-113 + 15q-112 + 16q-111 + 6q-110 - 12q-109 - 19q-108 - 11q-107 + 5q-106 + 19q-105 + 16q-104 + q-103 - 16q-102 - 20q-101 - 7q-100 + 13q-99 + 22q-98 + 11q-97 - 10q-96 - 23q-95 - 15q-94 + 8q-93 + 24q-92 + 18q-91 - 8q-90 - 25q-89 - 18q-88 + 7q-87 + 26q-86 + 20q-85 - 8q-84 - 26q-83 - 18q-82 + 7q-81 + 26q-80 + 20q-79 - 8q-78 - 27q-77 - 19q-76 + 7q-75 + 26q-74 + 20q-73 - 5q-72 - 25q-71 - 21q-70 + 4q-69 + 20q-68 + 18q-67 + 4q-66 - 14q-65 - 18q-64 - 7q-63 + 6q-62 + 11q-61 + 11q-60 + 3q-59 - 6q-58 - 10q-57 - 8q-56 - 2q-55 + 6q-54 + 8q-53 + 7q-52 - 7q-50 - 8q-49 - 2q-48 + q-47 + 5q-46 + 5q-45 - 2q-43 - q-42 - q-41 - q-40 + q-36 + q-35 + q-34 - q-33 - 2q-31 + q-28 + q-26 + q-15 |
| 6 | q-201 - q-200 - q-199 + q-196 + 3q-194 - 2q-192 - 2q-191 - 2q-190 - q-189 - q-188 + 5q-187 + 3q-186 + 2q-185 - q-183 - 3q-182 - 5q-181 - q-179 + q-177 + 4q-176 + 4q-175 + 4q-174 + 3q-173 - 2q-172 - 7q-171 - 11q-170 - 9q-169 - 2q-168 + 10q-167 + 15q-166 + 16q-165 + 9q-164 - 8q-163 - 23q-162 - 22q-161 - 9q-160 + 3q-159 + 19q-158 + 30q-157 + 17q-156 - 6q-155 - 16q-154 - 24q-153 - 24q-152 - 8q-151 + 21q-150 + 27q-149 + 19q-148 + 15q-147 - 8q-146 - 32q-145 - 36q-144 - 7q-143 + 10q-142 + 27q-141 + 41q-140 + 19q-139 - 18q-138 - 48q-137 - 30q-136 - 14q-135 + 21q-134 + 56q-133 + 40q-132 - 4q-131 - 52q-130 - 45q-129 - 28q-128 + 17q-127 + 64q-126 + 52q-125 + q-124 - 56q-123 - 51q-122 - 33q-121 + 18q-120 + 69q-119 + 55q-118 + q-117 - 59q-116 - 51q-115 - 34q-114 + 19q-113 + 70q-112 + 55q-111 - 60q-109 - 50q-108 - 33q-107 + 19q-106 + 70q-105 + 55q-104 + 2q-103 - 60q-102 - 53q-101 - 35q-100 + 18q-99 + 67q-98 + 57q-97 + 11q-96 - 51q-95 - 53q-94 - 44q-93 + 4q-92 + 51q-91 + 57q-90 + 31q-89 - 24q-88 - 38q-87 - 50q-86 - 21q-85 + 15q-84 + 39q-83 + 43q-82 + 10q-81 - 5q-80 - 33q-79 - 29q-78 - 19q-77 + 5q-76 + 25q-75 + 18q-74 + 17q-73 - 2q-72 - 8q-71 - 19q-70 - 10q-69 + q-68 + 6q-66 + 5q-65 + 8q-64 - 2q-63 + 2q-61 - 5q-60 - 6q-59 - 4q-58 + 2q-57 - q-56 + 3q-55 + 7q-54 + q-53 - q-52 - 2q-51 - 3q-49 - 2q-48 + 2q-47 + 2q-43 + q-40 - q-39 - 2q-37 + q-33 + q-31 + q-18 |
| 7 | - q-266 + q-265 + q-264 - q-261 - q-259 - 2q-258 + 2q-256 + 2q-255 + 3q-254 - 5q-250 - 4q-249 - 2q-248 + 3q-246 + 3q-245 + 3q-244 + 5q-243 + q-242 - 2q-240 - 5q-239 - 3q-238 - 3q-237 - 5q-236 - 3q-235 + q-234 + 4q-233 + 10q-232 + 8q-231 + 9q-230 + 8q-229 - 4q-228 - 15q-227 - 19q-226 - 19q-225 - 9q-224 + q-223 + 16q-222 + 34q-221 + 27q-220 + 14q-219 - 3q-218 - 23q-217 - 34q-216 - 35q-215 - 23q-214 + 7q-213 + 25q-212 + 34q-211 + 41q-210 + 23q-209 + 4q-208 - 23q-207 - 43q-206 - 40q-205 - 33q-204 - 11q-203 + 23q-202 + 44q-201 + 56q-200 + 46q-199 + 8q-198 - 27q-197 - 62q-196 - 72q-195 - 47q-194 - 4q-193 + 53q-192 + 87q-191 + 80q-190 + 37q-189 - 28q-188 - 89q-187 - 104q-186 - 71q-185 + 2q-184 + 81q-183 + 119q-182 + 99q-181 + 24q-180 - 69q-179 - 128q-178 - 119q-177 - 47q-176 + 57q-175 + 134q-174 + 134q-173 + 65q-172 - 49q-171 - 138q-170 - 146q-169 - 76q-168 + 45q-167 + 142q-166 + 153q-165 + 82q-164 - 42q-163 - 146q-162 - 158q-161 - 86q-160 + 43q-159 + 149q-158 + 159q-157 + 85q-156 - 43q-155 - 149q-154 - 160q-153 - 88q-152 + 45q-151 + 151q-150 + 160q-149 + 85q-148 - 44q-147 - 149q-146 - 160q-145 - 88q-144 + 45q-143 + 151q-142 + 160q-141 + 85q-140 - 44q-139 - 150q-138 - 161q-137 - 88q-136 + 45q-135 + 152q-134 + 161q-133 + 89q-132 - 39q-131 - 149q-130 - 165q-129 - 95q-128 + 33q-127 + 143q-126 + 160q-125 + 104q-124 - 11q-123 - 126q-122 - 157q-121 - 114q-120 - 10q-119 + 96q-118 + 137q-117 + 119q-116 + 43q-115 - 56q-114 - 109q-113 - 114q-112 - 68q-111 + 16q-110 + 66q-109 + 92q-108 + 78q-107 + 23q-106 - 23q-105 - 61q-104 - 66q-103 - 39q-102 - 13q-101 + 18q-100 + 45q-99 + 36q-98 + 28q-97 + 10q-96 - 11q-95 - 16q-94 - 28q-93 - 23q-92 - 8q-91 - 4q-90 + 6q-89 + 17q-88 + 18q-87 + 19q-86 + 4q-85 - 5q-84 - 5q-83 - 17q-82 - 16q-81 - 7q-80 + q-79 + 8q-78 + 6q-77 + 7q-76 + 9q-75 + 2q-74 - 4q-73 - 3q-72 - 3q-71 - q-70 - 6q-69 - 3q-68 + q-67 + 2q-66 + q-64 + 5q-63 + 4q-62 - q-61 - 2q-60 - q-59 - 2q-57 - 4q-56 + q-55 + 2q-54 + 2q-50 + q-49 - q-48 + q-46 - q-45 - 2q-43 + q-38 + q-36 + q-21 |
Computer Talk. The data above can be recomputed by Mathematica using the package KnotTheory`. Following setup, the sample Mathematica session below reproduces most of the above data (Mathematica system prompts in blue, human input in red, Mathematica output in black):
In[1]:= |
<< KnotTheory` |
Loading KnotTheory` (version of August 30, 2005, 10:15:35)... | |
In[2]:= | PD[Knot[10, 161]] |
Out[2]= | PD[X[1, 4, 2, 5], X[3, 12, 4, 13], X[7, 14, 8, 15], X[18, 9, 19, 10], > X[6, 19, 7, 20], X[16, 5, 17, 6], X[10, 17, 11, 18], X[13, 8, 14, 9], > X[20, 15, 1, 16], X[11, 2, 12, 3]] |
In[3]:= | GaussCode[Knot[10, 161]] |
Out[3]= | GaussCode[-1, 10, -2, 1, 6, -5, -3, 8, 4, -7, -10, 2, -8, 3, 9, -6, 7, -4, 5, > -9] |
In[4]:= | DTCode[Knot[10, 161]] |
Out[4]= | DTCode[4, 12, -16, 14, -18, 2, 8, -20, -10, -6] |
In[5]:= | br = BR[Knot[10, 161]] |
Out[5]= | BR[3, {-1, -1, -1, -2, 1, -2, -1, -1, -2, -2}] |
In[6]:= | {First[br], Crossings[br]} |
Out[6]= | {3, 10} |
In[7]:= | BraidIndex[Knot[10, 161]] |
Out[7]= | 3 |
In[8]:= | Show[DrawMorseLink[Knot[10, 161]]] |
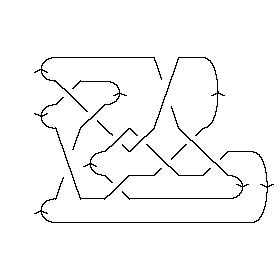 | |
Out[8]= | -Graphics- |
In[9]:= | #[Knot[10, 161]]& /@ {SymmetryType, UnknottingNumber, ThreeGenus, BridgeIndex, SuperBridgeIndex, NakanishiIndex} |
Out[9]= | {Reversible, 3, 3, 3, NotAvailable, 1} |
In[10]:= | alex = Alexander[Knot[10, 161]][t] |
Out[10]= | -3 2 3
3 + t - - - 2 t + t
t |
In[11]:= | Conway[Knot[10, 161]][z] |
Out[11]= | 2 4 6 1 + 7 z + 6 z + z |
In[12]:= | Select[AllKnots[], (alex === Alexander[#][t])&] |
Out[12]= | {Knot[10, 161]} |
In[13]:= | {KnotDet[Knot[10, 161]], KnotSignature[Knot[10, 161]]} |
Out[13]= | {5, -4} |
In[14]:= | Jones[Knot[10, 161]][q] |
Out[14]= | -11 -10 -9 -8 -7 -6 -3 -q + q - q + q - q + q + q |
In[15]:= | Select[AllKnots[], (J === Jones[#][q] || (J /. q-> 1/q) === Jones[#][q])&] |
Out[15]= | {Knot[10, 161]} |
In[16]:= | A2Invariant[Knot[10, 161]][q] |
Out[16]= | -34 -30 -28 -22 -18 -16 -14 -12 -10 -q - q - q + q + q + q + q + q + q |
In[17]:= | HOMFLYPT[Knot[10, 161]][a, z] |
Out[17]= | 6 8 10 6 2 8 2 10 2 6 4 6 6 3 a - a - a + 9 a z - a z - a z + 6 a z + a z |
In[18]:= | Kauffman[Knot[10, 161]][a, z] |
Out[18]= | 6 8 10 7 11 13 6 2 8 2 10 2
-3 a - a + a + 2 a z + a z + 3 a z + 9 a z + 3 a z - 3 a z +
12 2 7 3 11 3 13 3 6 4 8 4 10 4
> 3 a z - a z - 3 a z - 4 a z - 6 a z - a z + a z -
12 4 11 5 13 5 6 6 12 6
> 4 a z + a z + a z + a z + a z |
In[19]:= | {Vassiliev[2][Knot[10, 161]], Vassiliev[3][Knot[10, 161]]} |
Out[19]= | {7, -18} |
In[20]:= | Kh[Knot[10, 161]][q, t] |
Out[20]= | -7 -5 1 1 1 1 1 1 1
q + q + ------ + ------ + ------ + ------ + ------ + ------ + ------ +
23 9 19 8 19 7 17 6 15 6 17 5 15 5
q t q t q t q t q t q t q t
1 2 1 1 1 1
> ------ + ------ + ------ + ------ + ----- + -----
13 5 13 4 11 4 13 3 9 3 9 2
q t q t q t q t q t q t |
In[21]:= | ColouredJones[Knot[10, 161], 2][q] |
Out[21]= | -31 -30 -29 2 2 -25 -24 -23 -22 -21 2 2
q - q - q + --- - --- + q + q - q - q + q - --- + --- -
28 26 19 18
q q q q
2 -15 -14 -13 -11 -6
> --- + q + q - q + q + q
16
q |
| Dror Bar-Natan: The Knot Atlas: The Rolfsen Knot Table: The Knot 10161 |
|