© | Dror Bar-Natan: The Knot Atlas: 11 Crossing Knots:

K11n35 K11n37

Knotscape

This page is passe. Go here instead!    The Knot K11n36 Visit K11n36's page at Knotilus! Acknowledgement

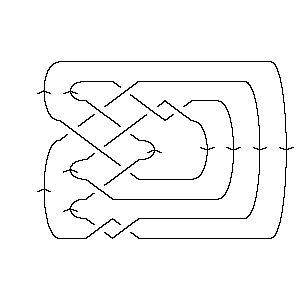DrawMorseLink

PD Presentation:

X4251 X8493 X5,13,6,12 X2837 X9,17,10,16 X11,18,12,19 X13,7,14,6 X15,20,16,21 X17,1,18,22 X19,14,20,15 X21,10,22,11

Gauss Code:

{1, -4, 2, -1, -3, 7, 4, -2, -5, 11, -6, 3, -7, 10, -8, 5, -9, 6, -10, 8, -11, 9}

DT (Dowker-Thistlethwaite) Code:

4 8 -12 2 -16 -18 -6 -20 -22 -14 -10

Alexander Polynomial:

- t-4 + 4t-3 - 8t-2 + 13t-1 - 15 + 13t - 8t2 + 4t3 - t4

Conway Polynomial:

1 + z2 - 4z4 - 4z6 - z8

Other knots with the same Alexander/Conway Polynomial:

{K11n44, ...}

Determinant and Signature:

{67, 2}

Jones Polynomial:

q-3 - 3q-2 + 6q-1 - 9 + 11q - 11q2 + 11q3 - 8q4 + 5q5 - 2q6

Other knots (up to mirrors) with the same Jones Polynomial:

{K11n7, K11n44, ...}

A2 (sl(3)) Invariant:

q-8 - q-6 + 2q-4 - q-2 + q2 - 3q4 + 3q6 - 2q8 + 3q10 + q12 + 2q16 - 2q18 - q22

HOMFLY-PT Polynomial:

- 2a-6 - a-6z2 + 5a-4 + 9a-4z2 + 5a-4z4 + a-4z6 - 4a-2 - 12a-2z2 - 13a-2z4 - 6a-2z6 - a-2z8 + 2 + 5z2 + 4z4 + z6

Kauffman Polynomial:

- 3a-7z + 3a-7z3 + 2a-6 - 5a-6z2 + 4a-6z4 + a-6z6 - 6a-5z + 13a-5z3 - 8a-5z5 + 4a-5z7 + 5a-4 - 16a-4z2 + 23a-4z4 - 14a-4z6 + 5a-4z8 - 6a-3z + 17a-3z3 - 14a-3z5 + 2a-3z7 + 2a-3z9 + 4a-2 - 18a-2z2 + 30a-2z4 - 27a-2z6 + 9a-2z8 - 5a-1z + 14a-1z3 - 15a-1z5 + a-1z7 + 2a-1z9 + 2 - 5z2 + 8z4 - 11z6 + 4z8 - 2az + 7az3 - 9az5 + 3az7 + 2a2z2 - 3a2z4 + a2z6

V2 and V3, the type 2 and 3 Vassiliev invariants:

{1, 3}

Khovanov Homology: (The squares with yellow highlighting are those on the "critical diagonals", where j-2r=s+1 or j-2r=s+1, where s=2 is the signature of 1136. Nonzero entries off the critical diagonals (if any exist) are highlighted in red.)

trqj r = -4 r = -3 r = -2 r = -1 r = 0 r = 1 r = 2 r = 3 r = 4 r = 5 j = 13                   2 j = 11                 3   j = 9               5 2   j = 7             6 3     j = 5           5 5       j = 3         6 6         j = 1       4 6           j = -1     2 5             j = -3   1 4               j = -5   2                 j = -7 1

Computer Talk. The data above can be recomputed by Mathematica using the package KnotTheory`. Following setup, the sample Mathematica session below reproduces most of the above data (Mathematica system prompts in blue, human input in red, Mathematica output in black):

In[1]:=	<< KnotTheory`
Loading KnotTheory` (version of August 30, 2005, 10:15:35)...
In[2]:=	Show[DrawMorseLink[Knot[11, NonAlternating, 36]]]
Out[2]=	-Graphics-
In[3]:=	PD[Knot[11, NonAlternating, 36]]
Out[3]=	PD[X[4, 2, 5, 1], X[8, 4, 9, 3], X[5, 13, 6, 12], X[2, 8, 3, 7], > X[9, 17, 10, 16], X[11, 18, 12, 19], X[13, 7, 14, 6], X[15, 20, 16, 21], > X[17, 1, 18, 22], X[19, 14, 20, 15], X[21, 10, 22, 11]]
In[4]:=	GaussCode[Knot[11, NonAlternating, 36]]
Out[4]=	GaussCode[1, -4, 2, -1, -3, 7, 4, -2, -5, 11, -6, 3, -7, 10, -8, 5, -9, 6, -10, > 8, -11, 9]
In[5]:=	DTCode[Knot[11, NonAlternating, 36]]
Out[5]=	DTCode[4, 8, -12, 2, -16, -18, -6, -20, -22, -14, -10]
In[6]:=	alex = Alexander[Knot[11, NonAlternating, 36]][t]
Out[6]=	-4 4 8 13 2 3 4 -15 - t + -- - -- + -- + 13 t - 8 t + 4 t - t 3 2 t t t
In[7]:=	Conway[Knot[11, NonAlternating, 36]][z]
Out[7]=	2 4 6 8 1 + z - 4 z - 4 z - z
In[8]:=	Select[AllKnots[], (alex === Alexander[#][t])&]
Out[8]=	{Knot[11, NonAlternating, 36], Knot[11, NonAlternating, 44]}
In[9]:=	{KnotDet[Knot[11, NonAlternating, 36]], KnotSignature[Knot[11, NonAlternating, 36]]}
Out[9]=	{67, 2}
In[10]:=	J=Jones[Knot[11, NonAlternating, 36]][q]
Out[10]=	-3 3 6 2 3 4 5 6 -9 + q - -- + - + 11 q - 11 q + 11 q - 8 q + 5 q - 2 q 2 q q
In[11]:=	Select[AllKnots[], (J === Jones[#][q] || (J /. q-> 1/q) === Jones[#][q])&]
Out[11]=	{Knot[11, NonAlternating, 7], Knot[11, NonAlternating, 36], > Knot[11, NonAlternating, 44]}
In[12]:=	A2Invariant[Knot[11, NonAlternating, 36]][q]
Out[12]=	-8 -6 2 -2 2 4 6 8 10 12 16 18 q - q + -- - q + q - 3 q + 3 q - 2 q + 3 q + q + 2 q - 2 q - 4 q 22 > q
In[13]:=	HOMFLYPT[Knot[11, NonAlternating, 36]][a, z]
Out[13]=	2 2 2 4 4 6 2 5 4 2 z 9 z 12 z 4 5 z 13 z 6 z 2 - -- + -- - -- + 5 z - -- + ---- - ----- + 4 z + ---- - ----- + z + -- - 6 4 2 6 4 2 4 2 4 a a a a a a a a a 6 8 6 z z > ---- - -- 2 2 a a
In[14]:=	Kauffman[Knot[11, NonAlternating, 36]][a, z]
Out[14]=	2 2 2 5 4 3 z 6 z 6 z 5 z 2 5 z 16 z 2 + -- + -- + -- - --- - --- - --- - --- - 2 a z - 5 z - ---- - ----- - 6 4 2 7 5 3 a 6 4 a a a a a a a a 2 3 3 3 3 4 18 z 2 2 3 z 13 z 17 z 14 z 3 4 4 z > ----- + 2 a z + ---- + ----- + ----- + ----- + 7 a z + 8 z + ---- + 2 7 5 3 a 6 a a a a a 4 4 5 5 5 6 23 z 30 z 2 4 8 z 14 z 15 z 5 6 z > ----- + ----- - 3 a z - ---- - ----- - ----- - 9 a z - 11 z + -- - 4 2 5 3 a 6 a a a a a 6 6 7 7 7 8 8 14 z 27 z 2 6 4 z 2 z z 7 8 5 z 9 z > ----- - ----- + a z + ---- + ---- + -- + 3 a z + 4 z + ---- + ---- + 4 2 5 3 a 4 2 a a a a a a 9 9 2 z 2 z > ---- + ---- 3 a a
In[15]:=	{Vassiliev[2][Knot[11, NonAlternating, 36]], Vassiliev[3][Knot[11, NonAlternating, 36]]}
Out[15]=	{1, 3}
In[16]:=	Kh[Knot[11, NonAlternating, 36]][q, t]
Out[16]=	3 1 2 1 4 2 5 4 q 3 6 q + 6 q + ----- + ----- + ----- + ----- + ---- + --- + --- + 6 q t + 7 4 5 3 3 3 3 2 2 q t t q t q t q t q t q t 5 5 2 7 2 7 3 9 3 9 4 11 4 > 5 q t + 5 q t + 6 q t + 3 q t + 5 q t + 2 q t + 3 q t + 13 5 > 2 q t

Dror Bar-Natan: The Knot Atlas: 11 Crossing Knots: The Knot K11n36

K11n35 K11n37