MULTIVARIABLE CALCULUS
COURSE 2005-2006
TEST #2. COURSE 2005-2006
UNIVERSITY OF TORONTO
DEPARTMENT OF MATHEMATICS
MAT 237 Y - MULTIVARIABLE CALCULUS
TEST #2. JANUARY 26, 2006
INSTRUCTIONS:
Write your name and your student number on the front page of each of your examination booklets.
Show and explain your work in all questions.
Use both sides of the papers, if necessary. Do not tear out any pages.
Do not use pencils. Only pen written answers will be considered for remarking.
No calculators or any other aids are permitted. Duration: 110 minutes.
1. (10 marks) Given that the equation z 3 x z y = 0 defines z as a function of x and y , show that
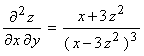 .
.
2. (10 marks) Determine all the points on the ellipsoid x 2 + 2 y 2 + 3 z 2 = 18 where the tangent plane is parallel to the plane x y 3 z = 1 , and find equations of each of the corresponding tangent planes.
3. (10 marks) Suppose that the functions f : R ฎ R and g : R ฎ R are both twice continuously differentiable and let
v ( x, y ) = f ( x 2 + 3 y ) + g ( x 2 3 y ) . Show that the function v satisfies the equation
x
3
![]() =
k (
=
k ( ![]()
x
x ![]() )
, where k is a constant, and find the value of the constant k
.
)
, where k is a constant, and find the value of the constant k
.
4. (10 marks) Consider the function f ( x , y ) = 2 x y + x 1 + 4 y 1 defined over the region
{ ( x , y ) ฮ R 2 ฝ x > 0 and y > 0 }. Find all the critical points of the function f . Classify each of the critical points of the function f as a local maximum, a local minimum or a saddle point. Show that the function f does not have an absolute maximum over the given region.
5. a) (10 marks) Suppose that f : R 3 ฎ R and g : R 3 ฎ R are both differentiable at a point ( a , b , c ) and that
f (
a , b , c ) is an extremum of the function f
subject to the constraint g ( x , y , z ) =
k , where k is a constant. Show that
![]() and
and
![]() .
.
b) (10 marks) Use part (a) above to find all extrema of f ( x , y , z ) = 4 x y + x z + 2 y z , subject to the constraint
x y z = 27 .
6. a) (10 marks) Compute the volume of the solid region enclosed between the paraboloids z = 3 x 2 + 3 y 2
and z = 12 x 2 y 2 .
b) (10 marks) Evaluate
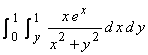 .
.
Hint for part (b): Remember that
![]() .
.
7. a) (10 marks) Suppose that the function f is
continuous over the interval [ a , b ] and the function
g is continuous over the interval [ c , d ] . Let h
( x , y ) = f ( x ) g ( y ) .
Show, using Riemann sums, that the function h is integrable over
the rectangle R = [ a , b ]
ด [ c
, d ]
and that ![]() .
.
Note: The text of this exercise requires the use of Riemann sums in the proof. So, you should not submit a proof in which the given property is viewed as an immediate consequence of Fubinis theorem.
b) (10 marks) Use part (a) above to evaluate the integral
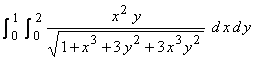 .
. ![]()
| TEST #2: 2005-06 (STATISTICS) |
|
HOME |
||
| TEST #1: 2002-03 | TEST #1: 2003-04 | TEST #1: 2004-05 |