MULTIVARIABLE CALCULUS
COURSE 2005-2006
SAMPLES OF PREVIOUS YEAR'S TESTS
TEST #1. COURSE 2002-2003.
1. a) (10 marks) Find an equation for the plane that passes through the point A ( 1 , 2 , 3 ) and contains the line ( x , y , z ) = ( 1 , 0 , 1 ) + t ( 1 , 1 , 1 ).
b) (10 marks) Let l1 be the line that passes through the origin and through the point with spherical coordinates ( r , q , f ) = ( 2 , 0 , p / 4 ) , and let l2 be the line that passes through the origin and through the point with spherical coordinates ( r , q , f ) = ( 2 , p / 4 , p / 2 ) . Find the angle between the lines l1 and l2 .
2. a) (10 marks) Find the distance from the point P ( 0 , - 2 , 6 ) to the plane that passes through the points A ( 1 , 0 , - 1 ) , B ( 1 , 2 , 0 ) , and C ( 0 , 2 , - 1 ) .
b) ( 10 marks) Find the coordinates of the point of the line ( x , y , z ) = ( 1 , - 2 , - 2 ) + t ( 1 , 1 , 0 ) which is closest to the line ( x , y , z ) = ( 1 , 3 , 2 ) + t ( 1 , 0 , 1 ) .
3. a) (10
marks) Consider the function
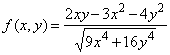 .
Show that
.
Show that
![]() does
not exist.
does
not exist.
b) (10 marks) Consider
the function
![]() .
Compute
.
Compute
![]() .
.
4. a) (10 marks) Find an equation of the plane that is tangent to the surface ( 2 x – y ) 3 + ( 2 y – z ) 3 = 2 at the point ( 1 , 1 , 1 ) .
b) (10
marks) Let f ( x , y ) = ( 3 y – x , 2
y – x y , y 2 ) , and let D
g ( u , v , w ) = ![]() .
.
Compute D ( g o f ) ( 2 , – 1 ) .
5. a) (10 marks) Suppose that a particle follows the path c ( t ) = ( e 1 - t , e t - 1 – 3 , t 2 ) until it flies off on a tangent at t = 1 . Determine the position of the particle at t = 3 .
b) (10 marks) Let f : R 2 ® R denote a function which is differentiable at the point P Î R 2 . Suppose that it is known that the directional derivative of the function f at the point P along the vector ( 4 / 5 , 3 / 5 ) is 1 , and the directional derivative of the function f at the point P along the vector ( 3 / 5 , - 4 / 5 ) is 2 . Give the unit vector u that indicates the direction of fastest increase of the given function f at the point P .
|
• HOME |
||
| • TEST #1: 2003-04 | • TEST #1: 2004-05 | • TEST #1: 2005-06 |