MULTIVARIABLE CALCULUS

COURSE 2005-2006

 TEST #1. COURSE 2005-2006

 UNIVERSITY OF TORONTO

DEPARTMENT OF MATHEMATICS

MAT 237 Y - MULTIVARIABLE CALCULUS

TEST #1. NOVEMBER 3, 2005

INSTRUCTIONS:

Write your name and your student number on the front page of each of your examination booklets.

Show and explain your work in all questions.

Use both sides of the papers, if necessary. Do not tear out any pages.

Do not use pencils. Only pen written answers will be considered for remarking.

No calculators or any other aids are permitted. Duration: 110 minutes.

1.  a) (8 marks) Compute the area of the region bounded by the curve   x = 2 + t ³ ,  y = 1 + t + 5 t ²  and the lines

x = 2 ,  x = 3  and  y = 0 .

b) (7 marks) Determine whether the curve  x = 2 t –  t ²  ,  y = 2 + 3 t – t ²  is concave upward or concave downward at the point  ( 0 , 4 ) .

2. (10 marks) Compute the length of the polar curve  r = sin ³ (q / 3 ) ,  0 £ q  £ 3 p / 4 .

3. (10 marks) Suppose that  a  and  b  are two non-zero vectors such that    and

 . Compute  .

4. (10 marks) Find the distance from the point  ( 2 , 0 , – 1 )  to the line of intersection of the planes

2 x + y = 1  and  y + z = 2 .

5. (10 marks) Let  L  be line that is tangent to the curve  x = 1 + t ² ,  y = 1 – t ,  z = 7 + t – t ² ,  at the point 

( 5 , 3 , 1 ) . Find the coordinates of the point of intersection of the line  L  and the plane  x – y = 8 .

6.  Suppose that  r ( t )  is a vector function such that  r ¢ ( t )  exists for all real numbers  t .

a) (7 marks) Let  f ( t ) =½r ( t )½⁵ . Determine the values of the constants  m  and  n , if any, for which

f ¢ ( t ) = m½r ( t )½ⁿ .

b) (8 marks) Let  v ( t ) = t ³ r ( t ) . Determine the polynomial function  p ( t ) , if any, for which

( r ( t ) + r ¢ ( t ) ) ´ v ¢ ( t ) = p ( t ) ( r ( t ) ´ r ¢ ( t ) ) .

7. Let  .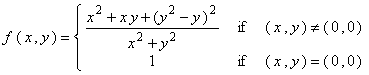

a) (7 marks) Show that the function  f  is not continuous at  ( 0 , 0 ) .

b) (8 marks) Compute  f _x ( 0 , 0 )  and  f _y ( 0 , 0 ) , if they exist .  

8. a) (10 marks) Prove that for any two sets  A  and  B  in  R ⁿ ,  int ( A Ç B ) = int ( A ) Ç int ( B ) .

Is it also true that for any two sets  A  and  B  in  R ⁿ ,  int ( A È B ) = int ( A ) È int ( B ) ?

b) (5 marks) Prove or disprove the following proposition:

If   f : C ® R ⁿ  is continuous, where  C Í R ^m  and  C  is closed, then  f ( C ) Í R ⁿ  is also closed.