MULTIVARIABLE CALCULUS

COURSE 2005-2006

SAMPLES OF PREVIOUS YEAR'S TESTS

TEST #3. COURSE 2002-2003.

 1. (15 marks) Evaluate  .

2. (15 marks) Evaluate   .

3. (15 marks) Compute the mass of the solid region defined by the inequalities

x ² + y ² ≤ z ≤ 8 - x ² - y ²  and  0 ≤ x ≤ y  if its density at any point  ( x , y , z )

is given by the function  d  ( x , y , z ) =  .

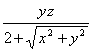4. (15 marks) Evaluate   , where  W  is the region in the first quadrant,

bounded by the curves  y = x ,  y = x + 4 ,  x y = 1 , and  x y = 3 .

Hint: Make the change of variables  x = - u + v ^{1 / 2}  and  y =  u + v ^{1 / 2} .

5. (15 marks) Compute the average  z-coordinate  of the points on the curve parametrized by

c ( t ) = ( t sin t , t cos t , t ³ / 6 ) ,  0 ≤ t ≤ 1 .

6. (15 marks) Evaluate the line integral   , where

F (x , y , z) = (y + e ^{– z} sin x) i + x j + (1 + e ^{– z} cos x) k , and

c ( t ) = ( ( 1 – t + t ² ) p , t ² , t ³ – 1 ) ,  0 ≤ t ≤ 1 .

7. (10 marks) Find a function  f , if any, such that for any real number  t :

.