MULTIVARIABLE CALCULUS

COURSE 2005-2006

SAMPLES OF PREVIOUS YEAR'S TESTS

TEST #3. COURSE 2003-2004.

1. (15 marks) Evaluate the line integral    where  C  is the curve of intersection of the surfaces

2 x + y = 5  and  x ² + z = 7  from the point  ( 0 , 5 , 7 )  to the point  ( 2 , 1 , 3 ) .

2. (15 marks) Consider the surface  S  in  R ³  parametrized by  F ( u , v ) = ( u cos v , u sin v , 2  )  with

0 £ u £ 1  and  0 £ v £ p . Compute   .

3. (15 marks) Evaluate the improper integral 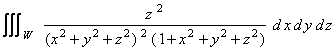  , where  W  is the

solid region consisting of all the points  ( x , y , z )  which are inside the cone 

but outside the sphere  x ² + y ² + z ² = 3 .

4. (20 marks) Evaluate the double integral   , where  R  is the region in the first quadrant,

enclosed between the curves  x y = 1  and  x y = 9  and between the lines  x = y   and  x = 16 y .

Hint: Make the change of variables  x = u v ,  y = u / v  with  u > 0  and  v > 0 .

5. (20 marks) Let  R  be the solid region defined by the conditions  0 £ z £ 2 –   and  x ² + y ² £ 2 y

and let  d ( x , y , z ) =   be its mass density at any point  ( x , y , z ) . Find the total mass of the solid  R .

6. (15 marks) Let  S  be the surface  a x ² + a y ² + z ² =  a , where  a  denotes a positive real number.

Suppose that  g ( a )  denotes the flux of the vector field  F ( x , y , z ) = x i + y j + a z k  out of the closed surface  S .

Find the value of  a , if any, for which  g ( a ) = 6 a p .