MULTIVARIABLE CALCULUS

COURSE 2005-2006

SAMPLES OF PREVIOUS YEAR'S TESTS

TEST #2. COURSE 2003-2004.

1. (15 marks) Find all the critical points of the function  f ( x , y ) = x ² y + 2 x y ² – 4 x y – 6  and use the second-derivative test to classify each of these critical points as a local minimum, a local maximum or a saddle point.

2. (15 marks) Find the absolute minimum and maximum values of the function  f ( x , y , z ) = 2 x y + z ³

over the region  x ² + 2 y ² + 3 z ² £ 12 ,  z ³ 0 .

3. (10 marks) Show that the system 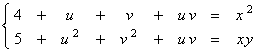    can be solved for  u  and  v

as functions of  x  and  y  near  ( u , v ) = ( 1 , 2 ) ,  ( x , y ) = ( 3 , 4 ) .

Find the value of    when  u = 1 ,  v = 2 ,  x = 3  and  y = 4 .

4. (10 marks) Let  C  denote the curve of intersection of the surfaces  x ² + y = 1  and  2 x ³ – 3 z = 27 .

Compute the length of the curve  C  from the point  ( 0 , 1 , – 9 )  to the point  ( 3 , – 8 , 9 ) .

5. (10 marks) Let  F ( x , y , z ) = .

Let  G = curl F ,  f = F × G  and  g = Ñ ² f . Compute  g ( 1 / 2 , 1 / 2 , 1 / 2 ) .

6. (15 marks) Change the order of integration and evaluate the integral   .  

7. (15 marks) Evaluate the triple integral  , where  W  is the solid region in the first octant

( x ³ 0 ,  y ³ 0  and  z ³ 0 )  bounded by the surfaces  y = 3 – x – z ² ,  y = 2 x  and  x = 0 .

8. (10 marks) Let  f ( t ) =  . Compute  f  ¢ ( 1 ) ,  f  ¢¢ ( 1 )  and  f  ¢¢¢ ( 1 ) .