MULTIVARIABLE CALCULUS
COURSE 2005-2006
SAMPLES OF PREVIOUS YEAR'S TESTS
TEST #1. COURSE 2003-2004.
1. Consider the vectors a = j - k , b = 2 i - 2 j + k , c = i + 4 j - 3 k , and d = i + 2 j .
a) (5 marks) Find the angle between the vectors a and b .
b) (5 marks) Find the area of the parallelogram spanned by the vectors c and d .
c) (5 marks) Find the volume of the parallelepiped spanned by the vectors a , b , and c .
2. a) (5 marks) Consider the surface described by the equation ( 1 + ( x – y ) 2 ) z = x ( 5 – 2 y z ) in Cartesian coordinates. Find an equation of the form z = f ( r , q ) to describe this surface using cylindrical coordinates. Find the value of z when r = 2 and q = p / 3 .
b) (5 marks) Consider the surface described by the equation x 2 + ( y – 1 ) 2 + 2 z 2 = 1 in Cartesian coordinates. Find an equation of the form r = g (q , f ) to describe this surface using spherical coordinates. Find the value of r when q = p / 3 and f = p / 2 .
3. (15 marks) Let S be the surface described by the equation 2 ( x 3 + y 3 – z 3 ) – ( x + y – z ) 3 = – 4 .
Let l be the line that is normal to the surface S at the point ( 1 , 0 , – 1 ) and let p be the plane that is tangent to the surface S at the point ( 1 , 1 , 0 ) . Find the coordinates of the point of intersection of the line l and the plane p .
4. a) (5 marks) State, without proof, the Triangle Inequality and the Cauchy-Schwarz Inequality for any vectors v and w in n .
b) (5 marks) Use both,
the Triangle Inequality and the Cauchy-Schwarz Inequality, to
show that the inequality ![]() holds
for any three vectors a , b , and c in
n
.
holds
for any three vectors a , b , and c in
n
.
5. a) (5 marks) Is the set A = { ( x , y ) Î 2 ½ y ¹ 0 } an open set? Briefly explain.
b) (5 marks)
Evaluate ![]() or
briefly explain why this limit does not exist.
or
briefly explain why this limit does not exist.
c) (5 marks)
Let 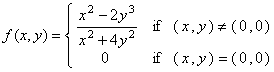 .
.
Compute ![]() or
briefly explain why this partial derivative does not exist.
or
briefly explain why this partial derivative does not exist.
d) (5 marks) Let f : 2 ® 2 and g : 2 ® 2 be differentiable functions, such that f ( 4 , 5 ) = ( 6 , 7 ) ,
D f ( 4 , 5 ) =
![]() ,
and
D g ( 6 , 7 ) =
,
and
D g ( 6 , 7 ) =
![]() .
Compute D
( g
o
f ) ( 4 , 5 ) .
.
Compute D
( g
o
f ) ( 4 , 5 ) .
6. (10 marks) Let w = x 3 + y 3 , where x = 2 s + 3 t and y = 3 s + 2 t .
Show that 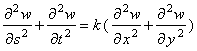 and
find the value of
the constant k .
and
find the value of
the constant k .
7. Let f :
2
®
be
a function whose first and second order partial
derivatives are continuous. Suppose that: f ( 0 , 1 ) = 5 ,
![]() ,
,
![]() ,
,
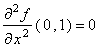 ,
,
![]() ,
and
,
and 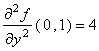 .
.
a) (10 marks) Determine the second-order Taylor formula for the function f at the point ( 0 , 1 ) and use it to find an approximated value for f ( 0.2 , 0.9 ) .
b) (10 marks) Let
u
Î
2
denote
a unit vector. Let g ( x , y ) denote the directional
derivative of the function f ( x , y ) along the
vector u and let h ( x , y ) denote the
directional derivative of the function
g ( x , y ) along the vector u
. Find all unit vectors u , if any, for which h ( 0 , 1 ) =
0 . (Hint: Represent the
unit vector as u = ( u 1 , u 2 )
, express h ( x , y ) in terms of u 1
, u 2 , 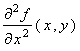 ,
,
![]() and
and
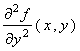 ,
then obtain h ( 0 , 1 ) in terms of u 1 and
u 2 .)
,
then obtain h ( 0 , 1 ) in terms of u 1 and
u 2 .)
|
• HOME |