UNIVERSITY OF TORONTO
DEPARTMENT OF MATHEMATICS
MAT 237 Y - MULTIVARIABLE CALCULUS
FALL-WINTER 2005-06
TEST #2. SOLUTIONS
1. Given that the equation z 3 x z y = 0 defines z as a function of x and y , show that
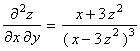 .
.
Soln.
![]() and
and
![]() .
.
Then,
 .
.
2. Determine all the points on the ellipsoid x 2 + 2 y 2 + 3 z 2 = 18 where the tangent plane is parallel to the plane
x y 3 z = 1 , and find equations of each of the corresponding tangent planes.
Soln. A vector normal to the given plane is n = ( 1 , 1 , 3 ) and a vector normal to the given ellipsoid at a point
( x , y , z ) on the ellipsoid is ั ( x 2 + 2 y 2 + 3 z 2 ) = ( 2 x , 4 y , 6 z ) .
For these two vectors to be parallel, we need ( 2 x , 4 y , 6 z ) = l ( 1 , 1 , 3 ) or
x = l / 2 , y = l / 4 and z = l / 2 .
Then, ( l / 2 ) 2 + 2 ( l / 4 ) 2 + 3 ( l / 2 ) 2 = 18 and l = ฑ 4 .
The points on the ellipsoid are ( 2 , 1 , 2 ) and ( 2 , 1 , 2 ) .
Equations for the corresponding tangent planes are x y 3 z = 9 and x y 3 z = 9 .
3. Suppose that the functions f : R ฎ R and g : R ฎ R are both twice continuously differentiable and let
v ( x, y ) = f ( x 2 + 3 y ) + g ( x 2 3 y ) .
Show that
the function v satisfies the equation x
3
![]() =
k (
=
k ( ![]()
x
x ![]() )
,
)
,
where k is a constant, and find the value of the constant k .
Soln.
![]() ,
,
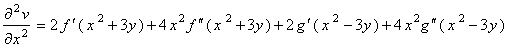 and
and
![]()
x
x ![]() =
=
![]() .
.
Also,
![]() ,
,
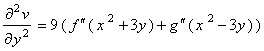 ,
and
,
and
 .
.
Therefore,
x
3
![]() =
=
![]() (
(
![]()
x
x ![]() )
and k = 9 / 4 .
)
and k = 9 / 4 .
4. Consider the function f ( x , y ) = 2 x y + x 1 + 4 y 1 defined over the region
{ ( x , y ) ฮ R 2 ฝ x > 0 and y > 0 }. Find all the critical points of the function f .
Classify each of the critical points of the function f as a local maximum, a local minimum or a saddle point.
Show that the function f does not have an absolute maximum over the given region.
Soln. f x ( x , y ) = 2 y x 2 and f y ( x , y ) = 2 x 4 y 2 .
The condition f x ( x , y ) = 0 = f y ( x , y ) implies y = x 2 / 2 and 2 x = 16 x 4 with x > 0 .
Then ( x , y ) = ( 1 / 2 , 2 ) is the only critical point.
Now, f x x ( x , y ) = 2 x 3 , f x y ( x , y ) = 2 and f y y ( x , y ) = 8 y 3 .
At ( x , y ) = ( 1 / 2 , 2 ) we have f x x ( 1 / 2 , 2 ) = 16 > 0 and
( f x x f y y ( f x y ) 2 ) ( 1 / 2 , 2 ) = ( 16 ) ( 1 ) 2 2 = 12 > 0 .
So, the function f has a local minimum at ( 1 / 2 , 2 ) .
This function does not have an absolute maximum over the given region.
In effect, for any M > 0 , take x = y = M 1 . Then, f ( M 1 , M 1 ) = 2 M 2 + 5 M > M .
5. a) Suppose that f : R 3 ฎ R and g : R 3 ฎ R are both differentiable at a point ( a , b , c ) and that
f ( a , b , c ) is an extremum of the function f subject to the constraint g ( x , y , z ) = k , where k is a constant.
Show that
![]() and
and
![]() .
.
Soln. If f ( a , b , c ) is an extremum of the function f subject to the constraint g ( x , y , z ) = k , then
ั f ( a , b , c ) = l ั g ( a , b , c ) , that is:
![]() ,
,
![]() and
and
![]() .
.
Using the first and third of the above equations to eliminate the parameter l , we obtain:
![]() .
.
Similarly, using now the second and the third equations to eliminate the parameter l , we obtain:
![]() .
.
b) Use part (a) above to find all extrema of f ( x , y , z ) = 4 x y + x z + 2 y z ,
subject to the constraint x y z = 27 .
Soln. In this case, ั f ( x , y , z ) = ( 4 y + z , 4 x + 2 z , x + 2 y ) and ั g ( x , y , z ) = ( y z , x z , x y ) .
Using part (a), we obtain the system of equations:
(i) ( 4 y + z ) ( x y ) ( x + 2 y ) ( y z ) = 0 and (ii) ( 4 x + 2 z ) ( x y ) ( x + 2 y ) ( x z ) = 0 ,
which simplify to (i) 2 y 2 ( 2 x z ) = 0 and (ii) x 2 ( 4 y z ) = 0 .
But x น 0 , y น 0 and z น 0 because x y z = 27 , then
(i) implies that z = 2 x , (ii) implies that z = 4 y and ( x , y , z ) = ( 3 , 3 / 2 , 6 ) .
The only extremum of the given function under the given constraint is f ( 3 , 3 / 2 , 6 ) = 54 .
 6.
a) Compute the volume of the solid region enclosed between the
6.
a) Compute the volume of the solid region enclosed between the
paraboloids z = 3 x 2 + 3 y 2 and z = 12 x 2 y 2 .
Soln. We use polar coordinates.
At the
intersection of the two paraboloids, 3 r
2
= 12 r
2
and ![]() .
.
Then,
![]()
=
![]() =
18
p
.
=
18
p
.
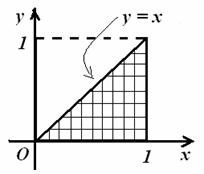 b)
Evaluate
b)
Evaluate 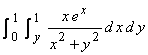 .
.
Hint for part (b): Remember that
![]() .
.
Soln.
The region of integration is ![]() ,
,
which can also
be described as ![]() .
Then,
.
Then,
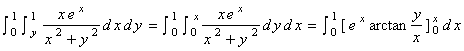
![]() .
.
7. a) Suppose that the function f is continuous over the interval [ a , b ] and the function g is continuous over the interval [ c , d ] . Let h ( x , y ) = f ( x ) g ( y ) .
Show, using Riemann sums, that the function h is integrable over the rectangle R = [ a , b ] ด [ c , d ]
and that ![]() .
.
Note: The text of this exercise requires the use of Riemann sums in the proof. So, you should not submit a proof in which the given property is viewed as an immediate consequence of Fubinis theorem.
Soln. Let P be a partition of the rectangle R and let S m n denote any of the Riemann sums of the function h over R with the partition P , then
S m n =
![]() ,
,
where ![]() with
x 0 = a < x 1 < x 2
<
< x m = b and
with
x 0 = a < x 1 < x 2
<
< x m = b and
![]() ,
,
with y 0 = c < y 1 < y 2 < < y n = d .
The functions f and g are both continuous over the corresponding intervals [ a , b ] and [ c , d ] .
Therefore, each of the intervals [ x i 1 , x i ] contains numbers t i and T i such that
f ( t i ) ≤ f ( x ) ≤ f ( T i ) for all x ฮ [ x i 1 , x i ] and each of the intervals [ y j 1 , y j ]
contains numbers w j and W j such that g ( w j ) ≤ g ( y ) ≤ g ( W j ) for all y ฮ [ y j 1 , y j ] .
Then,
![]() ,
,
where
![]()
are both Riemann sums of the function f over [ a , b ] and
![]()
are both Riemann sums of g over [ c , d ] .
Recall that ![]() is
just the limit of S m n as
is
just the limit of S m n as
max ( x i x i 1 ) ฎ 0 and max ( y j y j 1 ) ฎ 0 .
The functions f and g being continuous over [ a , b ] and [ c , d ] , respectively, are integrable over these intervals. Then, as max ( x i x i 1 ) ฎ 0 and max ( y j y j 1 ) ฎ 0 :
![]() ,
,
also
![]() ,
,
and therefore
![]() .
.
That is: the function h is integrable over R and
![]() .
.
b) Use part (a) above to evaluate the integral
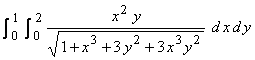 .
.
Soln.
Notice that 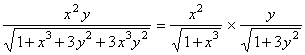 therefore,
therefore,
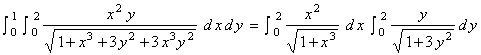
=![]() .
.
|
HOME |