© | Dror Bar-Natan: The Knot Atlas: The Thistlethwaite Link Table:

L10n110 L10n112

Knotscape

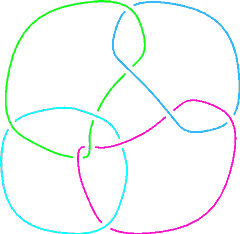
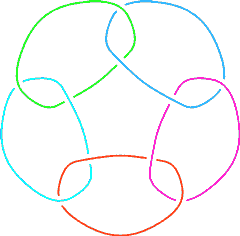
This page is passe. Go here instead! The 4-Component Link L10n111 Visit L10n111's page at Knotilus! Acknowledgement

DrawMorseLink

PD Presentation:

X6172 X12,3,13,4 X13,17,14,20 X19,11,20,16 X7,19,8,18 X15,8,16,9 X9,14,10,15 X17,5,18,10 X2536 X4,11,1,12

Gauss Code:

{{1, -9, 2, -10}, {-8, 5, -4, 3}, {9, -1, -5, 6, -7, 8}, {10, -2, -3, 7, -6, 4}}

Jones Polynomial:

- q-11/2 + q-9/2 - 2q-7/2 - q-5/2 - 2q-3/2 - 2q-1/2 - q3/2 + q5/2 - q7/2

A2 (sl(3)) Invariant:

q-18 + 2q-16 + 3q-14 + 5q-12 + 8q-10 + 12q-8 + 12q-6 + 12q-4 + 10q-2 + 7 + 5q2 + 2q4 + q6 + q12

HOMFLY-PT Polynomial:

- a-3z - a-1z-3 - 3a-1z-1 - 2a-1z + 3az-3 + 8az-1 + 10az + 6az3 + az5 - 3a3z-3 - 7a3z-1 - 8a3z - 2a3z3 + a5z-3 + 2a5z-1 + a5z

Kauffman Polynomial:

- 2a-3z + 4a-3z3 - a-3z5 - 2a-2z2 + 4a-2z4 - a-2z6 + a-1z-3 - 5a-1z-1 + 12a-1z - 11a-1z3 + 6a-1z5 - a-1z7 - 3z-2 + 10 - 20z2 + 13z4 - 2z6 + 3az-3 - 12az-1 + 35az - 43az3 + 21az5 - 3az7 - 6a2z-2 + 19a2 - 26a2z2 + 6a2z4 + 4a2z6 - a2z8 + 3a3z-3 - 12a3z-1 + 31a3z - 39a3z3 + 20a3z5 - 3a3z7 - 3a4z-2 + 10a4 - 8a4z2 - 3a4z4 + 5a4z6 - a4z8 + a5z-3 - 5a5z-1 + 10a5z - 11a5z3 + 6a5z5 - a5z7

Khovanov Homology:

trqj r = -6 r = -5 r = -4 r = -3 r = -2 r = -1 r = 0 r = 1 r = 2 r = 3 r = 4 j = 8                     1 j = 6                   1 1 j = 4               1 1     j = 2             1 1 1     j = 0           1 4 1       j = -2         2 1 3         j = -4       1 5 1           j = -6     1 1 3             j = -8   1 2                 j = -10                       j = -12 1

Computer Talk. The data above can be recomputed by Mathematica using the package KnotTheory`. Following setup, the sample Mathematica session below reproduces most of the above data (Mathematica system prompts in blue, human input in red, Mathematica output in black):

In[1]:=	<< KnotTheory`
Loading KnotTheory` (version of August 30, 2005, 10:15:35)...
In[2]:=	Length[Skeleton[L]]
Out[2]=	4
In[3]:=	Show[DrawMorseLink[Link[10, NonAlternating, 111]]]
Out[3]=	-Graphics-
In[4]:=	PD[L = Link[10, NonAlternating, 111]]
Out[4]=	PD[X[6, 1, 7, 2], X[12, 3, 13, 4], X[13, 17, 14, 20], X[19, 11, 20, 16], > X[7, 19, 8, 18], X[15, 8, 16, 9], X[9, 14, 10, 15], X[17, 5, 18, 10], > X[2, 5, 3, 6], X[4, 11, 1, 12]]
In[5]:=	GaussCode[L]
Out[5]=	GaussCode[{1, -9, 2, -10}, {-8, 5, -4, 3}, {9, -1, -5, 6, -7, 8}, > {10, -2, -3, 7, -6, 4}]
In[6]:=	Jones[L][q]
Out[6]=	-(11/2) -(9/2) 2 -(5/2) 2 2 3/2 5/2 7/2 -q + q - ---- - q - ---- - ------- - q + q - q 7/2 3/2 Sqrt[q] q q
In[7]:=	A2Invariant[L][q]
Out[7]=	-18 2 3 5 8 12 12 12 10 2 4 6 12 7 + q + --- + --- + --- + --- + -- + -- + -- + -- + 5 q + 2 q + q + q 16 14 12 10 8 6 4 2 q q q q q q q q
In[8]:=	HOMFLYPT[Link[10, NonAlternating, 111]][a, z]
Out[8]=	3 5 3 5 1 3 a 3 a a 3 8 a 7 a 2 a z 2 z -(----) + --- - ---- + -- - --- + --- - ---- + ---- - -- - --- + 10 a z - 3 3 3 3 a z z z z 3 a a z z z z a 3 5 3 3 3 5 > 8 a z + a z + 6 a z - 2 a z + a z
In[9]:=	Kauffman[Link[10, NonAlternating, 111]][a, z]
Out[9]=	3 5 2 4 2 4 1 3 a 3 a a 3 6 a 3 a 5 12 a 10 + 19 a + 10 a + ---- + --- + ---- + -- - -- - ---- - ---- - --- - ---- - 3 3 3 3 2 2 2 a z z a z z z z z z z 3 5 2 12 a 5 a 2 z 12 z 3 5 2 2 z > ----- - ---- - --- + ---- + 35 a z + 31 a z + 10 a z - 20 z - ---- - z z 3 a 2 a a 3 3 2 2 4 2 4 z 11 z 3 3 3 5 3 4 > 26 a z - 8 a z + ---- - ----- - 43 a z - 39 a z - 11 a z + 13 z + 3 a a 4 5 5 4 z 2 4 4 4 z 6 z 5 3 5 5 5 > ---- + 6 a z - 3 a z - -- + ---- + 21 a z + 20 a z + 6 a z - 2 3 a a a 6 7 6 z 2 6 4 6 z 7 3 7 5 7 2 8 > 2 z - -- + 4 a z + 5 a z - -- - 3 a z - 3 a z - a z - a z - 2 a a 4 8 > a z
In[10]:=	Kh[L][q, t]
Out[10]=	3 2 1 1 2 1 1 1 3 5 4 + -- + q + ------ + ----- + ----- + ----- + ----- + ----- + ----- + ----- + 2 12 6 8 5 8 4 6 4 6 3 4 3 6 2 4 2 q q t q t q t q t q t q t q t q t 2 1 1 1 2 4 2 2 4 2 6 3 6 4 > ----- + - + ---- + ---- + t + q t + q t + q t + q t + q t + q t + 2 2 t 4 2 q t q t q t 8 4 > q t

Dror Bar-Natan: The Knot Atlas: The Thistlethwaite Link Table: The Link L10n111

L10n110 L10n112