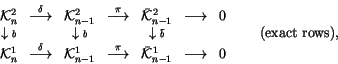We have so far found that if V is a type-n invariant, then
![]() is a linear functional on
is a linear functional on
![]() .
A question arises
whether every linear functional on
.
A question arises
whether every linear functional on
![]() arises in this way. At least
if the ground ring is extended to
arises in this way. At least
if the ground ring is extended to
![]() ,
the answer is positive:
,
the answer is positive:
The problem with the Fundamental Theorem is that all the proofs we have for it are somehow ``transcendental'', using notions from realms outside the present one, and none of the known proofs settles the question over the integers (see [BS]). In this section we describe what appears to be the most natural and oldest approach to the proof, having been mentioned already in [Va1,BL]. Presently, we are stuck and the so-called ``topological'' approach does not lead to a proof. But it seems to me that it's worth studying further; when something natural fails, there ought to be a natural reason for that, and it would be nice to know what it is.
The idea of the topological approach is simple: To get from W to
V, we need to ``integrate'' n times. Let's do this one integral at
a time. By the definition of
![]() ,
we know that we can integrate
once and find
,
we know that we can integrate
once and find
![]() so that
so that
![]() .
Can
we work a bit harder, and find a ``good'' W1, so that there would
be a
.
Can
we work a bit harder, and find a ``good'' W1, so that there would
be a
![]() with
with
![]() ? Proceeding like
that and assuming that all goes well along the way, we would end with a
? Proceeding like
that and assuming that all goes well along the way, we would end with a
![]() with
with
![]() ,
as required. Thus we are
naturally lead to the following conjecture, which implies the Fundamental
Theorem by the backward-inductive argument just sketched:
,
as required. Thus we are
naturally lead to the following conjecture, which implies the Fundamental
Theorem by the backward-inductive argument just sketched:
This conjecture is somewhat stronger than Theorem 2. Indeed, Theorem 2 is equivalent to Conjecture 1 restricted to the case when the given invariant has some (possibly high) derivative identically equal to 0(exercise!). But it is hard to imagine a topological proof of the restricted form of Conjecture 1 that would not prove it in full.
The difficulty in Conjecture 1 is that it's hard
to say much about
![]() .
In [Hu],
Michael Hutchings was able to translate the statement
.
In [Hu],
Michael Hutchings was able to translate the statement
![]() to an easier-looking
combinatorial-topological statement, which is implied by
and perhaps equivalent to an even simpler fully combinatorial
statement. Furthermore, Hutchings proved the fully combinatorial statement
in the analogous case of finite type braid invariants, thus proving
Conjecture 1 and Theorem 2
(over
to an easier-looking
combinatorial-topological statement, which is implied by
and perhaps equivalent to an even simpler fully combinatorial
statement. Furthermore, Hutchings proved the fully combinatorial statement
in the analogous case of finite type braid invariants, thus proving
Conjecture 1 and Theorem 2
(over
![]() )
in that case, and thus proving the viability of his
technique.
)
in that case, and thus proving the viability of his
technique.
Hutchings' first step was to write a chain of isomorphisms reducing
![]() to something more manageable. Our next step
will be to introduce all the spaces participating in Hutchings' chain.
First, let us consider the space of all T4T relations:
to something more manageable. Our next step
will be to introduce all the spaces participating in Hutchings' chain.
First, let us consider the space of all T4T relations:
The spaces
![]() form a ladder similar to the one
in (2), and, in fact, they combine with the ladder
in (2) to a single commutative diagram:
form a ladder similar to the one
in (2), and, in fact, they combine with the ladder
in (2) to a single commutative diagram:
In this language, Stanford's theorem (Theorem 1) says
that all L shapes in the above diagram (compositions
![]() of
``down'' followed by ``right'') are exact.
of
``down'' followed by ``right'') are exact.
Just like singular knots had symbols which were simplar combinatorial objects (chord diagrams), so do toplogical relators have combinatorial symbols:
The following proposition is proved along the same lines as the standard proof of Proposition 1.6.
We need to display one additional commutative diagram before we can come to Hutchings' chain of isomorphisms:
In this diagram, ![]() is the ``symbol level'' version of b, and
is induced by
is the ``symbol level'' version of b, and
is induced by
![]() in the usual manner. It
can be described combinatorially by
in the usual manner. It
can be described combinatorially by
![\begin{displaymath}\bar{b}:
\if ny
\smash{\makebox[0pt]{\hspace{-0.5in}
\rais...
...{-8pt}{ \input draws/barb.tex }
\hspace{-1.9mm}
\end{array}. \end{displaymath}](img76.gif)
Hutchings' chain of isomorphisms is the following chain of equalities and
maps: (here the symbol ![]() means that the space below is a subspace of
the space above, and the symbol
means that the space below is a subspace of
the space above, and the symbol
![]() means that the space below is a
sub-quotient of the space above)
means that the space below is a
sub-quotient of the space above)
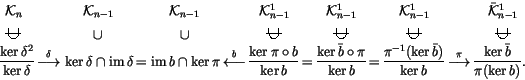
Proof. Immediate from diagrams (3)
and (4).
![]()
It doesn't look like we've achieved much, but in fact we did, as it
seems that
![]() is easier to digest than the
original space of interest,
is easier to digest than the
original space of interest,
![]() .
The point
is that
.
The point
is that
![]() lives fully in the combinatorial realm, being
essentially the space of all relations between 4T relations at the
symbol level. Similarly,
lives fully in the combinatorial realm, being
essentially the space of all relations between 4T relations at the
symbol level. Similarly,
![]() is the space of projections to the
symbol level of relation between 4T relations, and hence we have shown
is the space of projections to the
symbol level of relation between 4T relations, and hence we have shown
An obvious approach to proving Conjecture 1 thus emerges:
So far, the problem with this approach appears to be in the combinatorial
step. There is a conjectural generating set
![]() for
for
![]() .
Every element in
.
Every element in
![]() indeed
has a lifting to
indeed
has a lifting to ![]() ,
but we still don't know if
,
but we still don't know if
![]() indeed generates
indeed generates
![]() .
We state these facts very briefly; more
information can be found in [Hu] and
in [BS].
.
We state these facts very briefly; more
information can be found in [Hu] and
in [BS].
![\begin{eqnarray*}\bar b\left(
\if ny
\smash{\makebox[0pt]{\hspace{-0.5in}
\ra...
...pt}{ \input draws/bGExample.tex }
\hspace{-1.9mm}
\end{array}.
\end{eqnarray*}](img88.gif)
A parallel of Conjecture 2 for braids was proven by Hutchings in [Hu].