


Next: 1.4 Hutchings' theory of
Up: 1. The case of
Previous: 1.2 Constancy conditions, ,
Next, we wish to find conditions that a ``potential top derivative'' has
to satisfy in order to actually be a top derivative. More precisely, we
wish to find conditions that a functional
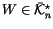 has
to satisfy in order to be
has
to satisfy in order to be
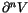 for some invariant V. A first
condition is that W must be ``integrable once''; namely, there has to
be some
for some invariant V. A first
condition is that W must be ``integrable once''; namely, there has to
be some
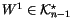 with
with
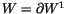 .
Another quick
glance at (2), and we see that W is integrable once iff
it vanishes on
.
Another quick
glance at (2), and we see that W is integrable once iff
it vanishes on
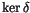 ,
which is the same as requiring that Wdescends to
,
which is the same as requiring that Wdescends to
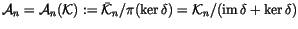 (there should be no confusion
regarding the identities of the
(there should be no confusion
regarding the identities of the 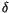 's involved). Often elements of
's involved). Often elements of
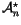 are refered to as ``weight systems''. A more accurate
name would be ``once-integrable weight systems''.
are refered to as ``weight systems''. A more accurate
name would be ``once-integrable weight systems''.
We see that it is necessary to understand
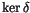 .
In
Figure 4 we show a family of members of
.
In
Figure 4 we show a family of members of
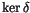 ,
the
``Topological 4-Term'' (T4T) relations. Figure 5 explains
how they arise from ``lassoing a singular point''. The following theorem
says that this is all:
,
the
``Topological 4-Term'' (T4T) relations. Figure 5 explains
how they arise from ``lassoing a singular point''. The following theorem
says that this is all:
Figure 4:
A Topological 4-Term (T4T) relation. Each of the four graphics in the
picture represents a part of an n-singular knot (so there are n-2 additional singular points not shown), and, as usual in knot theory, the
4 singular knots in the equation are the same outside the region shown.
![\begin{figure}\begin{displaymath}
\if ny
\smash{\makebox[0pt]{\hspace{-0.5in}
...
...put draws/T4T.tex }
\hspace{-1.9mm}
\end{array} \end{displaymath}
\end{figure}](img45.gif) |
Figure 5:
Lassoing a singular point: Each of the graphics represents an
(n-1)-singular knot, but only one of the singularities is explicitly
displayed. Start from the left-most graphic, pull the ``lasso'' under
the displayed singular point, ``lasso'' the singular point by crossing
each of the four arcs emenating from it one at a time, and pull the
lasso back out, returning to the initial position. Each time an arc is
crossed, the difference between ``before'' and ``after'' is the
co-derivative of an n-singular knot (up to signs). The four
n-singular knot thus obtained are the ones making the Topological
4-Term relation, and the co-derivative of their signed sum is the
difference between the first and the last (n-1)-singular knot shown
in this figure; namely, it is 0.
![\begin{figure}\begin{displaymath}
\if ny
\smash{\makebox[0pt]{\hspace{-0.5in}
...
...t draws/Lasso.tex }
\hspace{-1.9mm}
\end{array} \end{displaymath}
\end{figure}](img46.gif) |
Pushing the T4T relations down to the level of symbols, we get the
well-known 4T relations, which span
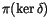 :
(see
e.g. [B-N1])
:
(see
e.g. [B-N1])
We thus find that
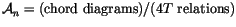 ,
as usual in the theory of finite type invariants of knots.
,
as usual in the theory of finite type invariants of knots.



Next: 1.4 Hutchings' theory of
Up: 1. The case of
Previous: 1.2 Constancy conditions, ,
Dror Bar-Natan
2000-03-19
![]() has
to satisfy in order to be
has
to satisfy in order to be
![]() for some invariant V. A first
condition is that W must be ``integrable once''; namely, there has to
be some
for some invariant V. A first
condition is that W must be ``integrable once''; namely, there has to
be some
![]() with
with
![]() .
Another quick
glance at (2), and we see that W is integrable once iff
it vanishes on
.
Another quick
glance at (2), and we see that W is integrable once iff
it vanishes on
![]() ,
which is the same as requiring that Wdescends to
,
which is the same as requiring that Wdescends to
![]() (there should be no confusion
regarding the identities of the
(there should be no confusion
regarding the identities of the ![]() 's involved). Often elements of
's involved). Often elements of
![]() are refered to as ``weight systems''. A more accurate
name would be ``once-integrable weight systems''.
are refered to as ``weight systems''. A more accurate
name would be ``once-integrable weight systems''.
![]() .
In
Figure 4 we show a family of members of
.
In
Figure 4 we show a family of members of
![]() ,
the
``Topological 4-Term'' (T4T) relations. Figure 5 explains
how they arise from ``lassoing a singular point''. The following theorem
says that this is all:
,
the
``Topological 4-Term'' (T4T) relations. Figure 5 explains
how they arise from ``lassoing a singular point''. The following theorem
says that this is all:
![\begin{figure}\begin{displaymath}
\if ny
\smash{\makebox[0pt]{\hspace{-0.5in}
...
...put draws/T4T.tex }
\hspace{-1.9mm}
\end{array} \end{displaymath}
\end{figure}](img45.gif)
![\begin{figure}\begin{displaymath}
\if ny
\smash{\makebox[0pt]{\hspace{-0.5in}
...
...t draws/Lasso.tex }
\hspace{-1.9mm}
\end{array} \end{displaymath}
\end{figure}](img46.gif)
![]() :
(see
e.g. [B-N1])
:
(see
e.g. [B-N1])
![\begin{displaymath}4T:\qquad
\if ny
\smash{\makebox[0pt]{\hspace{-0.5in}
\rai...
...ox{-8pt}{ \input draws/4T.tex }
\hspace{-1.9mm}
\end{array}. \end{displaymath}](img48.gif)
![]() ,
as usual in the theory of finite type invariants of knots.
,
as usual in the theory of finite type invariants of knots.