


Next: 1.3 Integrability conditions, ,
Up: 1. The case of
Previous: 1.1 Singular knots, the
As promised in the introduction, we study invariants of type n by
studying their nth derivatives. Clearly, if V is of type n and
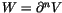 ,
then
,
then
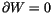 (``W is a constant''). Glancing
at (2), we see that W descends to a linear functional,
also called W, on
(``W is a constant''). Glancing
at (2), we see that W descends to a linear functional,
also called W, on
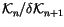 :
:
Definition 1.5
We call
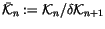
the space of ``
n-symbols'' associated with the ladders
in (
2). (The name is inspired by the theory of differential
operators, where the ``symbol'' of an operator is essentially its
equivalence class modulo lower order operators. The symbol is responsible
for many of the properties of the original operator, and for many
purposes, two operators that have the same symbol are ``the same''.)
We denote the projection mapping
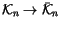
that maps every
singular knot to its symbol by
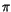
.
The following classical proposition (see e.g. [B-N1,Bi,BL,Go1,Go2,Ko1,Va1,Va2] identifies the space of n-symbols in our case:
Proposition 1.6
The space
of
n-symbols for (
2) is
canonically isomorphic to the space
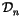
of
n-chord diagrams,
defined below.

Definition 1.7
An
n-chord diagram is a choice of
n pairs of
distinct points on an oriented circle, considered up to orientation
preserving homeomorphisms of the circle. Usually an
n-chord diagram is
simply drawn as a circle with
n chords (whose ends are the
n pairs),
as in the 5-chord example in Figure
3. The space
is the space of all formal

-linear combinations of
n-chord diagrams.
Figure 3:
A chord diagram.
![\begin{figure}\begin{displaymath}
\if ny
\smash{\makebox[0pt]{\hspace{-0.5in}
...
...draws/5Chords.tex }
\hspace{-1.9mm}
\end{array} \end{displaymath}
\end{figure}](img37.gif) |



Next: 1.3 Integrability conditions, ,
Up: 1. The case of
Previous: 1.1 Singular knots, the
Dror Bar-Natan
2000-03-19
![]() ,
then
,
then
![]() (``W is a constant''). Glancing
at (2), we see that W descends to a linear functional,
also called W, on
(``W is a constant''). Glancing
at (2), we see that W descends to a linear functional,
also called W, on
![]() :
: