1.5 Summary

In summary, we have introduced and studied the following objects, spaces, and maps:

Objects: ${\mathcal O}={\mathcal K}$ is the space of all framed oriented knots in an oriented ${\mathbb R}^3$. More precisely, it is the free ${\mathbb Z}$-module generated by framed oriented knots in an oriented ${\mathbb R}^3$.

The n-Cubes: ${\mathcal O}_n={\mathcal K}_n$ is the free ${\mathbb Z}$-module generated by framed oriented knots in an oriented ${\mathbb R}^3$, that have precisely n double point singularities $\left(\doublepoint\right)$ as in Figure 2, modulo the co-differentiability relation of Definition 1.2,

$$\if ny \smash{\makebox[0pt]{\hspace{-0.5in} \raisebox{8pt}{... ...8pt}{ \input draws/codiff.tex } \hspace{-1.9mm} \end{array}.$$

The Co-Derivative: The co-derivative $\delta:{\mathcal O}_{n+1}\to{\mathcal O}_n$ is the map $\delta:{\mathcal K}_{n+1}\to{\mathcal K}_n$ defined by

$$\if ny \smash{\makebox[0pt]{\hspace{-0.5in} \raisebox{8pt}{... ...t}{ \input draws/deltadef.tex } \hspace{-1.9mm} \end{array}.$$

The Cube Ladder and Finite Type Invariants:

The n-Symbols: The space of n-symbols ${\mathcal O}_n/\delta{\mathcal O}_{n+1}$ is the space ${\mathcal K}_n/\delta{\mathcal K}_{n+1}$ of n-chord diagrams, as in Figure 3.

The Relator Ladder: The relator ladder is the ladder

$${ \begin{array}{ccccccc} \ldots\stackrel{\delta}{\longrig... ...-1} & \stackrel{\delta}{\longrightarrow}\ldots, \end{array}}$$

(see Equation 3), of singular knots with exactly one ``Topological Relator'' singularity as in Figure 6.

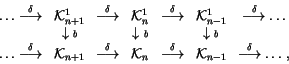
The Primary Integrability Constraints: The primary integrability constraints are the images of the relators via the map b; that is, they are the Topological 4-Term relations of Figure 4.

The Relator Symbols and the Symbol-Level Relations: The relator symbols are diagrams of the kind appearing in Figure 7.

The Once-Reduced Symbol Space and Once Integrable Weight Systems:

The Inductive Problem:

The Lifting Problem:

Generic Symbol-Level Redundencies:

The Object-Level Redundencies:

The Redundency Problem: