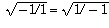
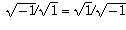
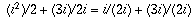 ,
,
The Fallacious Proof:
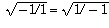
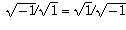
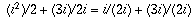 ,
,
See how many tries it takes you to correctly identify the fallacious step!
The complex numbers are a set of objects that includes not only the familiar real numbers but also an additional object called "i". Addition and multiplication are defined on this larger set in such a way that i^2 = -1. So, although -1 does not have any square root within the context of real numbers, but it does have a square root within the larger context of complex numbers.
One thing that often confuses people is the question "what is this strange object i"? There are different ways to define it, all essentially equivalent. One convenient way is to define complex numbers to be pairs (a,b) of real numbers. Addition is defined by the rule (a,b) + (c,d) = (a+c, b+d), and multiplication is defined by the strange-looking rule (a,b)(c,d) = (ac-bd, ad+bc).
With this definition, a complex number of the form (a,0) is identical in all its arithmetic properties to the real number a, and is therefore just a different way of representing the same abstract concept that the real number a does. So it is legitimate to think of the complex number (a,0) and the real number a as being "the same thing", and with this understanding, the complex numbers are a set of objects that contains the real numbers along with other things.
(This is exactly the same thing that one does when one first learns about rational numbers (fractions). A fraction is a pair of integers (a,b), commonly written as a/b. There are rules for addition: a/b + c/d = (ad+bc)/(bd) and for multiplication: (a/b)(c/d) = (ac)/(bd). With these rules, a fraction of the form a/1 behaves identically to the integer a, so we consider the rational number a/1 and the integer a to be "the same thing", and with this understanding, the rational numbers are a set of objects that contains the integers along with other things).
Having defined complex numbers as pairs of real numbers, we define i to be the pair (0,1). If you apply the above rule of multiplication, you find that (0,1)(0,1) = (-1,0) (which, remember, is really the same thing as the real number -1). In other words, i^2 = -1.
Finally, where did the above rule for multiplication come from? It came from the following reasoning:
We want to have in our set an object called i whose square is -1. We also want to have the usual real numbers in our set. We want a way to add and multiply elements in our set, so as well as i and the usual real numbers we also need to have all sums and products involving i and real numbers; in other words, for each pair (a,b) of real numbers, there needs to be a corresponding element a+bi in our set.
So, since to every pair of real numbers (a,b) there needs to correspond an element in our set, why don't we just let our set be the set of all pairs of real numbers. Now, what should our rule for multiplication be? We want addition and multiplication to satisfy the familiar properties of commutativity, distributivity, and associativity. That means (a + bi) + (c + di) should equal (a+c) + (b+d)i, and (a+bi)(c+di) should equal ac + bci + adi + bdi^2 = (ac-bd) + (bc+ad)i.
This reasoning says that there is only one possible way to define addition and multiplication and still have any hope at all of them satisfying the properties we want. That's why one makes the definition above. Then, having made that definition, one proves that this definition does in fact have all the properties we want. That's a separate exercise.