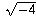 is 2i, what one means by
is 2i, what one means by
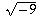 is 3i, etc. Once one has said that,
establishing exactly what the notation means,
then this part of the proof is perfectly valid.
is 3i, etc. Once one has said that,
establishing exactly what the notation means,
then this part of the proof is perfectly valid.
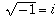 .
.
Strictly speaking, this depends upon exactly what one means by the square root symbol, which really is only defined for positive numbers.
However, there's nothing to stop one saying that, in this proof, what will
be meant by the square root symbol when applied to a negative number
is one of its two complex square roots, namely, the one that's a positive
multiple of i. So, for example, one could say that what one means
by 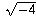 is 2i, what one means by
is 2i, what one means by
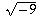 is 3i, etc. Once one has said that,
establishing exactly what the notation means,
then this part of the proof is perfectly valid.
is 3i, etc. Once one has said that,
establishing exactly what the notation means,
then this part of the proof is perfectly valid.
In summary: you've found a slight mistake in the proof (the fact that it was never specified exactly what the square root symbols is supposed to mean in this context), but it's an easily correctable mistake and not the source of the fallacy.
In fact, this mistake did not originate with this step in the proof, but crept in earlier. See if you can figure out where, as well as figuring out the step where the fallacy lies!