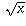This step is not the source of the fallacy.

However, you HAVE found a mistake!

There's a mistake in this step of the proof because the square root symbol only has an unambiguous meaning when applied to positive numbers.

When x is positive, it has two square roots: one positive, and one negative. By convention, the square root symbol 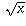is defined to mean the positive one.

But that convention won't work when x is a negative number. For instance, the two square roots of -1 are i and -i; these cannot be distinguished on the basis of "positive" and "negative", so how do we know which one is being meant by ?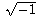

Therefore, it's not clear what is being meant by this step of the proof.

However, this mistake is not the source of the fallacy. The mistake can be corrected simply by specifying which square root is meant, for instance, saying that

when x is negative, we are using the notation to stand for the square root which is a positive multiple of i, rather than the other one which is a negative multiple of i.

To understand this, imagine a different culture where they use the symbol "j" for what we call "-i", and they use "-j" for what we call "i". There is nothing that makes our terminology any better than theirs; i and -i cannot be distinguished by any arithmetical properties.

In their culture, they'd probably still use 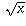to mean the positive root when x is positive, just like us (positive roots have different arithmetical properties than the negative ones do, so their culture and ours would agree about which is positive and which is negative). But they might adopt the opposite convention from us when x is negative, using 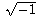to mean j (our -i).

So the convention of letting 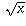refer to the positive root when x is positive does not necessarily imply any convention about what it should refer to when x is negative. That's why it's necessary to say in the proof which square root is being meant.