© | Dror Bar-Natan: Knot Atlas: KnotTheory`:               This page is passe. Go here instead!

Subsections

• 5.1.1 How does it work?

5.1 Drawing Planar Diagrams

My summer student Emily Redelmeier is in the process of writing a program that uses circle packing to draw an arbitrary object given as a PD as in Section 4.1. At the moment her program is still slow, limited and sometimes buggy, but it is already quite useful, as the following lines show:

In[1]

In[2]:= ?DrawPD
DrawPD[pd] takes the planar diagram description pd and creates a graphics object containing a picture of the knot. DrawPD[pd,options], where options is a list of rules, allows the user to control some of the parameters. OuterFace->n sets the face at infinity to the face numbered n. OuterFace->{e_1,e_2,...,e_n} sets the face at infinity to a face which has edges e_1, e_2, ..., e_n in the planar diagram description. Gap->g sets the size of the gap around a crossing to length g.

In[3]:= DrawPD::about
DrawPD was written by Emily Redelmeier at the University of Toronto in the summers of 2003 and 2004.

Thus, for example, here's the torus knot T(4,3):

In[4]:=	Show[DrawPD[TorusKnot[4, 3]]]
Out[4]=	-Graphics-

One problem we currently have is that crossings come out at non-uniform sizes, hence in the picture below you may need magnifying glasses to decide who's over and who's under:

In[5]:=

MillettUnknot = PD[ X[1,10,2,11], X[9,2,10,3], X[3,7,4,6], X[15,5,16,4], X[5,17,6,16], X[7,14,8,15], X[8,18,9,17], X[11,18,12,19], X[19,12,20,13], X[13,20,14,1] ];

In[6]:=	Show[DrawPD[MillettUnknot]]
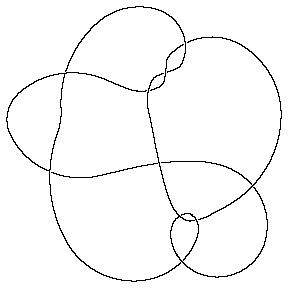Out[6]=	-Graphics-

In such a situation, the option Gap is sometimes handy:

In[7]:=	Show[DrawPD[MillettUnknot, {Gap -> 0.03}]]
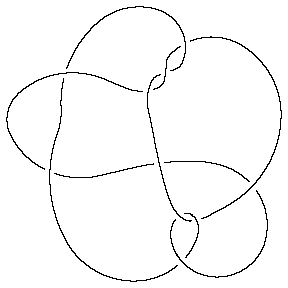Out[7]=	-Graphics-

5.1.1 How does it work?

DrawPD uses Andreev's theorem [An1,An2], which states that every planar graph can be realized, nearly uniquely, as the graph of tangencies of circles drawn within the unit disk. That is, to every vertex of $G$ one may associate a disk within the unit disk, so that the interiors of these disks are disjoint and they are tangent iff the corresponding vertices are connected by an edge. The Andreev ``circle packing'' corresponding to the knot $4_1$ is the left half of the picture below (circle $13$ is the unit disk itself).

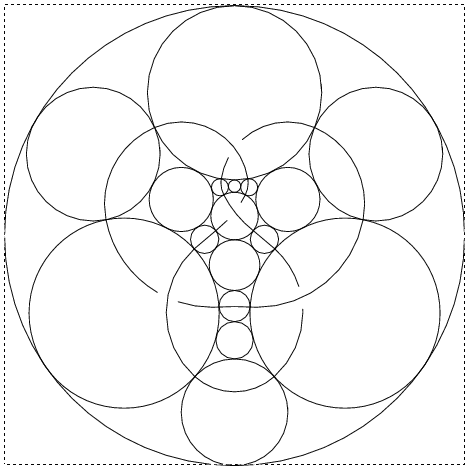But now every ingredient of the original knot (every arc, crossing and face) has a disk in the plane in which it can be cleanly drawn and clashes are guaranteed not to occur. Furthermore, knowing the precise coordinates of all the tangency points allows us to represent each ingredient by some nice smooth arcs that meet smoothly. The result is the right half of the picture above. Removing all the circles, what remains is the desired clean planar picture of $4_1$.