Algebraic Structures on Knotted Objects and Universal Finite Type Invariants

Dror Bar-Natan and Dylan P. Thurston

Date: This Edition: Jul. 23, 2001; Revision History: Section 6.1.

Abstract:

We discuss a number of topics related to algebraic constructions of universal finite type invariants. The idea is to find presentations of knot theory, or of some mild generalizations of knot theory, in terms of finitely many generators and relations, and then to construct a universal finite type invariant by setting its values on the generators so as the relations are satisfied. One such presentation involves knotted trivalent graphs, and is genuinely 3-dimensional. 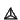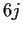In this presentation the generators turns out to be the standardly embedded tetrahedron $\tetrahedron$ and the relations are on one hand equivalent to the pentagon and hexagon relations of Drinfel'd's theory of associators and on the other hand they are closely related to the Biedenharn-Elliot identities of $6j$-symbols and to the Pachner moves of the theory of triangulations. Another such presentation involves Jones' notion of a planar algebra [J] and leads to a crossing-centric constructions of a universal finite type invariant (as opposed to the now-standard associativity-centric construction). Much of what we discuss is work in progress, and this article contains many ``live ends'', unfinished problems that don't seem to be dead ends.

Alternative formats
Sizes	232Kb	144Kb	464Kb	728Kb

The version exists in a SPLIT edition (about 32 html files and 151 images) for easier browsing, in a LONG edition (one html file, about 151 images) for easier searching and printing, and in a TAR.GZ version (232Kb) for offline browsing.