1.2 Generators, relations and syzygies

Summary. As a toy model for the algebraic approach to the construction of $Z$, we give a brief introduction to generators, relations and syzygies in a group-theoretical context, and their use in the construction of group representations.

As we have already mentioned, there are many approaches to the construction of an invariant $Z:{\mathcal K}({\circlearrowleft})\to{\mathcal A}({\circlearrowleft})$ satisfying the condition in Equation (2). The algebraic approach, which is the topic of this article, is to find some algebraic context within which the set ${\mathcal K}({\circlearrowleft})$ (or some mild generalization thereof) is finitely presented, and then to use this finite presentation to define $Z$. Namely, one would have to make wise guesses $Z(K_i)$ for the values of $Z$ on the generators $K_i$ of ${\mathcal K}({\circlearrowleft})$, so that for each relation $R_j(K_1,\ldots)$ the corresponding values of $Z$ would satisfy the corresponding relation $R_j(Z(K_1),\ldots)$ (two comments: 1. For this to make sense ${\mathcal A}({\circlearrowleft})$ must carry the same kind of algebraic structure as ${\mathcal K}({\circlearrowleft})$; 2. The verification of essentiality, Equation (2), is typically easy).

Let us see what this entails on a toy model. Suppose we want to find invariants of elements of the set $B_4$ of braids on 4 strands. One way to proceed is to notice that $B_4$ carries an algebraic structure, that is, it has an associative product which makes it a group. Thus we may seek invariants on $B_4$ with values in associative algebras, which respect the algebraic structure. Such creatures are not new on the mathematical scenery; they are usually called ``group representations''. Our approach to finding representations of $B_4$ would be to make wise guesses for their values $Z(\sigma_1)$, $Z(\sigma_2)$ and $Z(\sigma_3)$ on the generators $\sigma _1$, $\sigma _2$ and $\sigma _3$ of $B_4$ (see Figure 1), so as to satisfy the relations between the $\sigma _i$'s. Setting $z_i:=Z(\sigma_i)$, these relations are (again see Figure 1):

$$z_1z_3=z_3z_1,\quad z_1z_2z_1=z_2z_1z_2 \quad z_2z_3z_2=z_3z_2z_3.$$ (3)

Figure 1: A finite presentation of the group $B_4$ and one of its syzygies. The central frame in this figure shows the generators $\sigma _1$, $\sigma _2$ and $\sigma _3$ of $B_4$ followed by a standard way of writing the relations between them. The outside frame shows a syzygy between these relations -- a closed loop whose vertices are words in the generators $\sigma _i$ and whose edges are relations. See Comment 6.1.

In our real problem, the construction of $Z:{\mathcal K}({\circlearrowleft})\to{\mathcal A}({\circlearrowleft})$, the target space ${\mathcal A}({\circlearrowleft})$ is graded, and we will attempt to construct $Z$ inductively, degree by degree. Thus we will be asking ourselves, ``suppose our construction is done to degree 16; can we extend it to degree 17?''. Let us go back to the toy model and examine the situation over there. Let $A$ be an associative algebra and let $J\subset I\subset A$ be ideals in $A$ (think `` $I=\{$degrees$\geq 17\}$ and $J=\{$degrees$>17\}$'') so that $I\cdot I\subset J$ (``$17+17>17$''). Suppose we have $z_i\in A$ which satisfy the equations (3) in $A/I$ (``done to degree 16''). But equations (3) may fail in $A/J$; let $\lambda, \psi_a, \psi_b\in I/J$ be the errors in when these equations are considered in $A/J$:

$$\lambda:=z_1z_3-z_3z_1,\quad \psi_a:=z_1z_2z_1-z_2z_1z_2 \quad \psi_b:=z_2z_3z_2-z_3z_2z_3.$$ (4)

We wish to modify the $z_i$'s so as to satisfy equations (3) in $A/J$ (``extend to degree 17''), so we set

$$z'_i=z_i+\zeta_i\in A/J,$$ (5)

where we assume that $\zeta_i\in I/J$ (so as $z_i=z'_i$ in $A/I$) (``the correction $\zeta_i$ is of degree precisely 17''). We now compute the new errors $\lambda',\psi'_a,\psi'_b\in I/J$ in terms of the old ones and using the property $I\cdot I\subset J$:

$$\lambda' := z'_1z'_3-z'_3z'_1 = (z_1+\zeta_1)(z_3+\zeta_3)-(z_3+\zeta_3)(z_1+\zeta_1)$$ (6)

$$= z_1z_3-z_3z_1+z_1\zeta_3+\zeta_1z_3-z_3\zeta_1-\zeta_3z_1$$

$$= \lambda + \zeta_1z_3 + z_1\zeta_3 - \zeta_3z_1 - z_3\zeta_1,$$

and likewise,

$$\psi'_a = \psi_a + \zeta_1z_2z_1 + z_1\zeta_2z_1 + z_1z_2\zeta_1 - \zeta_2z_1z_2 - z_2\zeta_1z_2 - z_2z_1\zeta_2,$$

$$\psi'_b = \psi_b + \zeta_2z_3z_2 + z_2\zeta_3z_2 + z_2z_3\zeta_2 - \zeta_3z_2z_3 - z_3\zeta_2z_3 - z_3z_2\zeta_3.$$

These are linear equations, and thus to solve our problem, namely to find $\zeta_i$'s so that $\lambda'=\psi'_a=\psi'_b=0$, we need to show that the triple $E:=(\lambda,\psi_a,\psi_b)\in A^3$ is in the image of the linear map $d^r:A^3\to A^3$ defined by

$$d^r: \left(\begin{array}{c} \zeta_1 \zeta_2 \zeta_3 \end{... ...z_3\zeta_2 - \zeta_3z_2z_3 - z_3\zeta_2z_3 - z_3z_2\zeta_3 \end{array}\right).$$

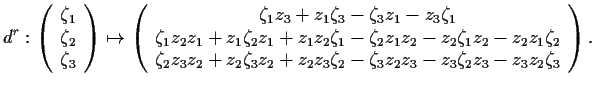
Our strategy to show that $E\in\operatorname{im}d^r$ is to find a second linear map $d^s$, whose domain is the target space of $d^r$, so that $d^s\circ d^r=0$ and so that $d^sE=0$. This done we can define the homology group $H:=\ker d^s/\operatorname{im}d^r$, and if by some magical means we could prove that it vanishes, we would use $d^sE=0$ to determine that $E\in\operatorname{im}d^r$, and our problem would be solved. We will mention techniques for the computation of the homology group $H$ in Section 5. For now we only wish to describe how the map $d^s$ is found.

To find linear relations between the errors $\lambda$, $\psi_a$ and $\psi_b$, we start with a syzygy for our presentation of the braid group $B_4$ -- a closed loop whose vertices are words in the generators $\sigma _i$ and whose edges are relations. When we perform the replacement $\sigma_i\to z_i$ on the vertices of a syzygy, say the one displayed in Figure 1, we get a loop like such:

$$\xymatrix @C=0.8in{ z_1z_2z_1z_3z_2z_1 \ar[r]_{-z_1z_2\lambda z_2... ... \ar[l]_{\psi_bz_1z_2z_3} & z_3z_2z_1z_3z_2z_3 \ar[l]_{-z_3z_2\lambda z_2z_3} }$$ (7)

Now given that the edges of a syzygy are relations, we know that the difference between the element written at the head of any given edge and at the tail of that edge is a multiple of $\lambda$, $\psi_a$ or $\psi_b$. These multiples are written to the side of each edge in Equation (7). By the ouroboros summation formula (a cousin of the telescopic summation formula, but where the beginning point and the end point are the same) the sum of these differences is 0. That is, $E$ is in the kernel of the linear map $d^s$ defined by

$$d^s: E=\left( \begin{array}{c} \lambda \psi_a \psi_b \end... ...z_2\lambda +z_2\lambda z_2z_3z_1 +z_2z_1\psi_bz_1 +\psi_az_3z_2z_1. \end{array}$$

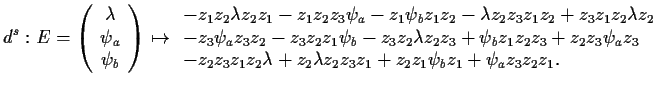
Moral. It would be nice to have an algebraic context within which knot theory is finitely presented and within which the syzygies of the presentation are simple to analyze.

Problem 1.1   In the specific case of the presentation of Figure 1 of the braid group $B_4$ (and its obvious generalization to $B_n$), we don't know if the methodology of this section can actually be used to construct invariants (though we do know of some more complecated situations in which this methodology is useful; see the rest of this article). This is especially interesting when the target algebra $A$ is taken to be the algebra ${\mathcal A}^b_n$ of chord diagrams for braids (see e.g. [BN4]).