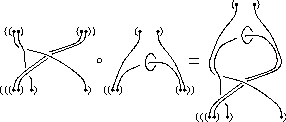 The category
PaT of ``parenthesized tangles'', (the algebraic structure
which we wish to represent, like
The category
PaT of ``parenthesized tangles'', (the algebraic structure
which we wish to represent, like
Summary. As an example where the scheme of Section 1.2 has been successfully used, and also in order to display some formulas for later use in this article, we give a very quick reminder of parenthesized tangles and the pentagon and hexagon relations and their syzygies, along the lines of [BN3,BN5,LM].
The papers [BN3,BN5,LM] introduce an algebraic context within which the scheme of Section 1.2 is used to construct a universal finite type invariants of links. The ``algebraic context'' there is the structure of a category with certain additional operations. Rather than defining everything in full, we will just recall some key notions, pictures and formulas here.
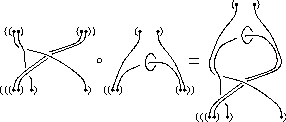 The category
PaT of ``parenthesized tangles'', (the algebraic structure
which we wish to represent, like
The category
PaT of ``parenthesized tangles'', (the algebraic structure
which we wish to represent, like ![]() in
Section 1.2) is the category whose objects are parenthesizations such as
in
Section 1.2) is the category whose objects are parenthesizations such as
![]() or
or
![]() , and whose morphisms are tangles with
parenthesized top and bottom. See the picture on the right, which also
illustrates how parenthesized tangles are composed.
, and whose morphisms are tangles with
parenthesized top and bottom. See the picture on the right, which also
illustrates how parenthesized tangles are composed.
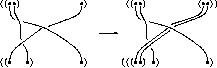 The category
PaT carries some additional
operations. The most interesting are the ``strand addition on the
left/right'' operations, and the strand doubling operations
(illustrated on the right). More details are in [BN3,BN5,LM].
The category
PaT carries some additional
operations. The most interesting are the ``strand addition on the
left/right'' operations, and the strand doubling operations
(illustrated on the right). More details are in [BN3,BN5,LM].
Likewise, one can set up a category
Pa![]() of ``parenthesized chord
diagrams'', that captures the ``symbols'' of ``singular'' parenthesized
tangles as in Equation (1). The category
Pa
of ``parenthesized chord
diagrams'', that captures the ``symbols'' of ``singular'' parenthesized
tangles as in Equation (1). The category
Pa![]() supports the same
additional operations as
PaT, and one may wish to look for structure
preserving functors
supports the same
additional operations as
PaT, and one may wish to look for structure
preserving functors
![]() PaT
PaT![]() Pa
Pa![]() which are ``essential'' in a sense
similar to that of Equation (2).
In [BN3], this is done following the same
generators-relations-syzygies sequence as in
Section 1.2:
which are ``essential'' in a sense
similar to that of Equation (2).
In [BN3], this is done following the same
generators-relations-syzygies sequence as in
Section 1.2:
Now let us assume that we already found ![]() and
and ![]() so that the
relations between them corresponding to
so that the
relations between them corresponding to ![]() and
and
![]() are
satisfied up to degree 16 (say), and let
are
satisfied up to degree 16 (say), and let ![]() and
and ![]() be the degree
17 errors in these equations (compare with Equation (4)).
That is, modulo degrees 18 and up we have (notaion as
in [BN3], compare with [BN3, Equations (10)
and (11)]):
be the degree
17 errors in these equations (compare with Equation (4)).
That is, modulo degrees 18 and up we have (notaion as
in [BN3], compare with [BN3, Equations (10)
and (11)]):
Proceeding as in Equation (5) we set
![]() and
and ![]() with
with ![]() and
and ![]() of
degree 17, and like in Equation (6) we get (compare
with [BN3, Equations (12) and (13)]):
of
degree 17, and like in Equation (6) we get (compare
with [BN3, Equations (12) and (13)]):
Thus we are interested in knowing whether the triple
![]() is
in the image of the linear map
is
in the image of the linear map
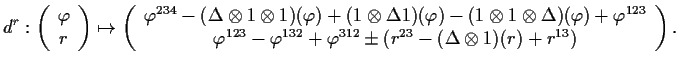
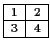 ; the
symbol
; the
symbol
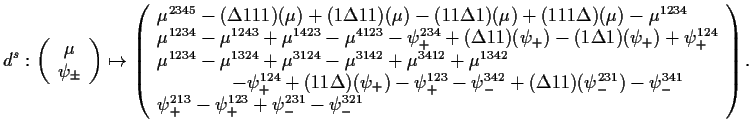
 |