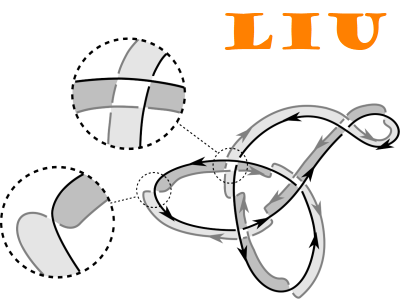
In 2018 Kashaev introduced a diagrammatic link invariant conjectured to be twice the Levine-Tristram signature. If true, the conjecture would provide a simple way of computing the Levine-Tristram signature of a link by taking the signature of a real symmetric matrix associated with a corresponding link diagram. This paper establishes the conjecture using the Seifert surface definition of the Levine-Tristram signature on the disjoint union of an oriented link and its reverse. The proof also reveals yet another formula for the Alexander polynomial.Her paper is at arXiv:2311.01923.

This is a summary of various determinant formulas for the Alexander polynomial, along with their implementations in Mathematica using the KnotTheory` package.His writeup is here, and the code is here.
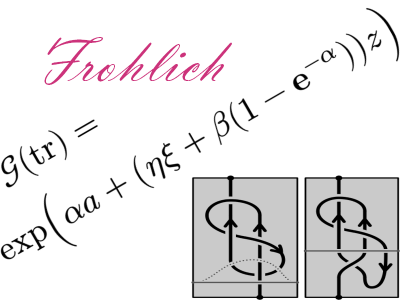
A well-known source of knot invariants is representations of quasitriangular Hopf algebras (also known as quantum groups). These invariants require exponential time in the number of crossings to compute. Recent work has allowed for polynomial-time computations within the Hopf algebras themselves, using perturbed Gaussian differential operators. This thesis introduces and explores a partial expansion of the tangle invariant $Z$ introduced by Bar-Natan and van der Veen. We expand the use of the Hopf algebra ${\mathfrak U}({\mathfrak s\mathfrak l}^0_{2+})$ to include its space of coinvariants, providing an extension $Z^{tr}$ of $Z$ from open tangles to links.His thesis is here.We compute a basis for the space of coinvariants of ${\mathfrak U}({\mathfrak s\mathfrak l}^0_{2+})$ and a closed-form expression for the exponential generating function of the corresponding trace map. The resulting function is not directly compatible with the previous research, so we also find a method of computing $Z^{tr}$ on a subclass of links and write a program to compute $Z^{tr}$ on two-component links. Contrary to expectations, we find that $Z^{tr}$ is neither stronger nor weaker than the Multivariable Alexander polynomial. This unexplained behaviour warrants further study into $Z^{tr}$ and its relationship with other invariants.
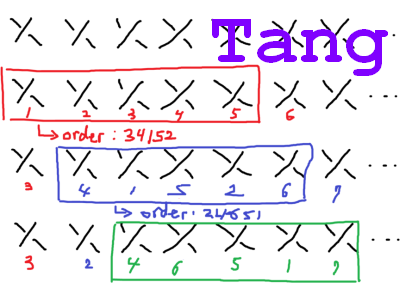
In knot theory, one problem of interest is to reduce the run time of calculating knot invariants such as the Jones' polynomial. One thing we can do is to seek to reduce the amount of information that we need to process through each time we add a crossing into the calculation by permuting the order of the crossings, which often is the only information needed to calculate knot invariants.See his report here, and his programs and data files here.
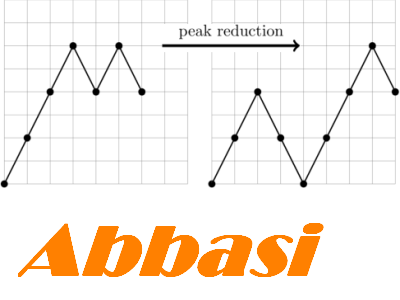
In 1947, Artin found a representation of the braid group on n strands in the automorphism group of the free group with n generators, and proved his representation is faithful. In 1986, McCool proved a theorem giving a presentation for the group of basis-conjugating automorphisms of the free group with n generators. McCool's theorem can be reinterpreted as the statement that a natural analogue of Artin's representation of the braid group is a faithful representation of the pure welded braid group on n strands. However, the proof of McCool's theorem uses Whitehead's peak reduction lemma, which has no interpretation in the context of welded braids. In this paper, we apply a version of Whitehead's peak reduction lemma suited for welded braids in order to obtain a simpler proof of McCool's theorem.See his project here.
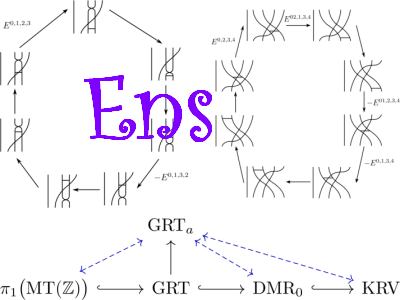
We develop the theory of braidors, an analogue of Drinfel'd's theory of associators in which braids in an annulus are considered rather than braids in a disk. After defining braidors and showing they exist, we prove that a braidor is defined by a single equation, an analogue of a well-known theorem of Furusho [Furusho (2010)] in the case of associators. Next some progress towards an analogue of another key theorem, due to Drinfel'd [Drinfel'd (1991)] in the case of associators, is presented. The desired result in the annular case is that braidors can be constructed degree be degree. Integral to these results are annular versions GTa and GRTa of the Grothendieck-Teichmuller groups GT and GRT which act faithfully and transitively on the space of braidors. We conclude by providing surprising computational evidence that there is a bijection between the space of braidors and associators and that the annular versions of the Grothendieck-Teichmuller groups are in fact isomorphic to the usual versions potentially providing a new and in some ways simpler description of these important groups, although these computations rely on the unproven result to be meaningful.See his thesis here.

See those notes as well as the accompanying Cheat Sheet.
Also visit Calder's blog.
See A Tabulation of Ribbon Knots in Tangle Form and The 250 Knots with up to 10 Crossings.
Also visit Andrey at GitHub.

Visit Torus Knot Fibrations. (Also see a possibly-outdated local copy and some source files).
Also visit Jesse's home page!
My Talk
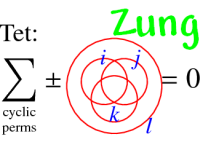
I will describe my former student's Jonathan Zung work on finite type invariants of "doodles", plane curves modulo the second Reidemeister move but not modulo the third. We use a definition of "finite type" different from Arnold's and more along the lines of Goussarov's "Interdependent Modifications", and come to a conjectural combinatorial description of the set of all such invariants. We then describe how to construct many such invariants (though perhaps not all) using a certain class of 2-dimensional "configuration space integrals".
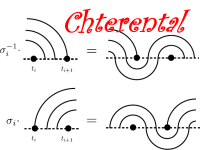
Chterental's Paper
This paper defines a faithful action of the virtual braid group vBn on certain planar diagrams called virtual curve diagrams. Our action is similar in spirit to the Artin action of the braid group Bn on the free group Fn and it provides an easy combinatorial solution to the word problem in vBn.Oleg's 2015 PhD thesis is available here.
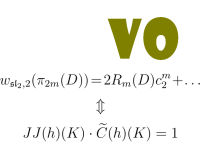
Our Paper
In this article, we show that a conjecture raised in [KLMR] (arXiv:1307.4933), which regards the coefficient of the highest term when we evaluate the sl2 weight system on the projection of a diagram to primitive elements, is equivalent to the Melvin-Morton-Rozansky conjecture, proved in [BNG] (MMR).

Our Paper.
We introduce a new invariant of tangles along with an algebraic framework in which to understand it. We claim that the invariant contains the classical Alexander polynomial of knots and its multivariable extension to links. We argue that of the computationally efficient members of the family of Alexander invariants, it is the most meaningful.
arXiv: 1209.4589
Virtual knot theory, introduced by Kauffman, is a generalization of usual knot theory which interests us because of its potential to be a topological interpretation of Etingof and Kazhdan's theory of quantization of Lie bi-algebras. Usual knots inject into virtual knots, and flat virtual knots is the quotient of virtual knots which equates the real positive and negative crossings, and so in this sense is complementary to usual knot theory within virtual knot theory. We classify flat virtual pure tangles, and give bases for the "infinitesimal" algebras of two of its variants. The classification of flat virtual pure tangles can be used as an invariant on virtual pure tangles.
Peter's Home Page.
If an augmented algebra K over Q is filtered by powers of its augmentation ideal I, the associated graded algebra grIK need not in general be quadratic: although it is generated in degree 1, its relations may not be generated by homogeneous relations of degree 2. In this paper we give a criterion which is equivalent to grIK being quadratic. We apply this criterion to the group algebra of the pure virtual braid group (also known as the quasi-triangular group), and show that the corresponding associated graded algebra is quadratic.See a video of Peter's lecture on the subject in November 2011.
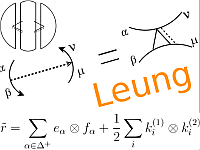
arXiv:0812.2342.
In 2002 Haviv gave a way of assigning Lie tensors to directed trivalent graphs. Weight systems on oriented chord idagrams modulo 6T can then be constructed from such tensors. In this paper we give explicit combinatorial formulas of weight systems using Manin triples constrcted from classical Lie algebras. We then compose these oriented weight systems with the averaging map to get weight systems on unoriented chord diagrams and show that they are the same as the ones obtained by Bar-Natan in 1991. In the last section we carry out calculations on certain examples.
Also visit our joint 2009 paper Some Dimensions of Spaces of Finite Type Invariants of Virtual Knots.
Louis' 2010 PhD thesis is Classical Lie Algebra Weight Systems of Arrow Diagrams.
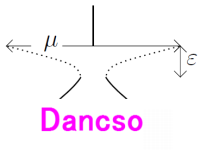
arXiv:0811.4615.
We construct an extension of the Kontsevich integral of knots to knotted trivalent graphs, which commutes with orientation switches, edge deletions, edge unzips, and connected sums. In 1997 Murakami and Ohtsuki first constructed such an extension, building on Drinfel'd's theory of associators. We construct a step by step definition, using elementary Kontsevich integral methods, to get a one-parameter family of corrections that all yield invariants well behaved under the graph operations above.
Also see Zsuzsanna on YouTube!
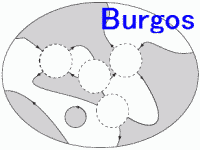
arXiv:0807.2600.
It is a well known result from Thistlethwaite that the Jones polynomial of a non-split alternating link is alternating. We find the "right" generalization of this result to the case of non-split alternating tangles. More specifically: the Jones polynomial of tangles is valued in a certain skein module, we describe an alternating condition on elements of this skein module, show that it is satisfied by the Jones invariant of the tangles consisting of a single overcrossing or a single undercrossing, and prove that it is preserved by appropriately "alternating" planar algebra compositions. Hence, this condition is satisfied by the Jones polynomial of all alternating tangles. Finally, in the case of 0-tangles, that is links, our condition is equivalent to simple alternation of the coefficients of the Jones polynomial.
Also visit Hernando's home page!

"Rubberband" Brunnian Links
Prime Links with a Non-Prime Component
Identifying Knots within a List
Burau's Theorem
Cabling
- A program to play with "Rubberband" Brunnian Links.
- Programs to find sublinks of a given link and as an application, to find prime link with non-prime components.
- A program to identify an unknown knot within a given list of knots.
- A program to compute the cables of a given knot and as an application, a test of Burau's theorem on cabling and the Alexander polynomial.
Also visit our joint 2009 paper Some Dimensions of Spaces of Finite Type Invariants of Virtual Knots.
Also visit Iva Halacheva's home page!
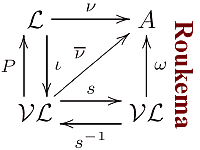
arXiv:0711.4001
Goussarov, Polyak, and Viro proved that finite type invariants of knots are "finitely multi-local", meaning that on a knot diagram, sums of quantities, defined by local information, determine the value of the knot invariant. The result implies the existence of Gauss diagram combinatorial formulas for finite type invariants. This article presents a simplified account of the original approach. The simplifications provide an easy generalization to the cases of pure tangles and pure braids. The associated problem on group algebras is introduced and used to prove the existence of "multi-local word formulas" for finite type invariants of pure braids.
Also visit our joint 2009 paper Some Dimensions of Spaces of Finite Type Invariants of Virtual Knots.

Seifert Surface Animation

Braid Representatives
The Multivariable Alexander Polynomial
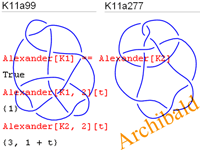
The Alexander-Conway Polynomial
See also her October 2007 article "The Weight System of the Multivariable Alexander Polynomial", arXiv:0710.4885.
See also her Ph.D. thesis, titled "The Multivariable Alexander Polynomial on Tangles".
Drawing MorseLink Presentations
DT (Dowker-Thistlethwaite) Codes
R-Matrix Invariants
The Coloured Jones Polynomials
- Programs to find and draw Morse Link presentations of knots and links.
- Programs to convert between Gauss Codes / DT codes and other knot presentations.
- Programs to compute general R-Matrix invariants of knots and links.
- A program to compute the coloured Jones polynomial of a knot.

A Table of Virtual Knots
More by Jeremy Green: JavaKh, a very fast and very general java program to compute Khovanov homology.
Virtual knot theory is an extension of knot theory which allows for virtual crossings, which are not over or under, in a diagram. In addition to the Reidemeister moves for classical crossings, moves involving virtual crossings are allowed. For details, see Louis Kauffman, Virtual Knot Theory, Europ. J. Combinatorics (1999) 20, 663-691, arXiv:math.GT/9811028.
This table of virtual knots was generated using a computer program written by Jeremy Green under the supervision of Dror Bar-Natan. The program generates a list of Gauss codes, then, via Reidemeister moves, determines which are equivalent to each other. Using an Athlon XP 2500+ with 512 MB RAM, the enumeration can be done up to 8 crossing oriented virtual knots, using 10 GB of disk, in about 24 hours. This 8 crossing enumeration is only useful for knots up to 6 crossings because of the need for higher crossing intermediates when finding relationships. This enumeration counted 725854 oriented virtual knots with up to 6 crossings, or 92800 when counting inverses and mirror images as the same knot.
The program also generates all of the content on the individual pages for the virtual knots, including the drawings and the various invariants. ...
To see the table, read more about it and download the programs, use the link on the left.
arXiv:0706.3680.
Earlier work by Gad Naot: arXiv:math.GT/0310366, titled "On Chern-Simons theory with an inhomogeneous gauge group and BF theory knot invariants" and arXiv:math.GT/0603347, titled "On the Algebraic Structure of Bar-Natan's Universal Geometric Complex and the Geometric Structure of Khovanov Link Homology Theories".
We explore the complex associated to a link in the geometric formalism of Khovanov's (n=2) link homology theory, determine its exact underlying algebraic structure and find its precise universality properties for link homology functors. We present new methods of extracting all known link homology theories directly from this universal complex, and determine its relative strength as a link invariant by specifying the amount of information held within the complex.We achieve these goals by finding a complex isomorphism which reduces the complex into one in a simpler category. We introduce few tools and methods, including surface classification modulo the 4TU/S/T relations and genus generating operators, and use them to explore the relation between the geometric complex and its underlying algebraic structure. We identify the universal topological quantum field theory (TQFT) that can be used to create link homology and find that it is "smaller" than what was previously reported by Khovanov. We find new homology theories that hold a controlled amount of information relative to the known ones.
The universal complex is computable efficiently using our reduction theorem. This allows us to explore the phenomenological aspects of link homology theory through the eyes of the universal complex in order to explain and unify various phenomena (such as torsion and thickness). The universal theory also enables us to state results regarding specific link homology theories derived from it. The methods developed in this thesis can be combined with other known techniques (such as link homology spectral sequences) or used in the various extensions of Khovanov link homology (such as sl3 link homology).
To read his thesis, use the link on the left.
Drawing Planar Diagrams
The Planar Enumerator Page.
There is a significant number of interesting topological objects that are enumerated by decorated planar graphs modulo "simple" planar relations. These include: knots and links (enumerated by quadrivalent planar graphs with over/under crossing information indicated, modulo "Reidemeister moves"), tangles, knotted graphs, wave fronts, 2D surfaces in R4 (via their Yoshikawa-style "central frames") and many more.
Some of these planar enumeration problems were studied extensively: e.g., there is vast literature on knot enumeration. Other such problems were just barely tackled: e.g., the current known enumeration of 2D surfaces in R4 fits in one page. Throughout my work in topology I have encountered a number of further enumeration problems of the same kind and wished I had had such an enumeration ready, if even rough and dirty and partial.
The purpose of Stephen's project is to write a general purpose program, "The Planar Enumerator", for rough and dirty enumeration. It will have no chance of competing with the existing knot enumeration, it is likely to beat the known 2D in R^4 enumeration, and what's best, it will be completely general and whenever a planar enumeration problem will come up, it will be simple to code it in the language of "The Planar Enumerator" and get the first few pages of tables ready.
The project is still at protype stage. See the link on the left.
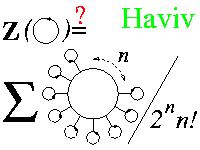
arXiv:math.QA/0211031
By considering spaces of directed Jacobi diagrams, we construct a diagrammatic version of the Etingof-Kazhdan quantization of complex semisimple Lie algebras. This diagrammatic quantization is used to provide a construction of a directed version of the Kontsevich integral, denoted ZEK, in a way which is analogous to the construction of the Reshetikhin-Turaev invariants from the R-matrices of the Drinfel'd-Jimbo quantum groups. Based on this analogy, we conjecture (and prove in a restricted sense) a formula for the value of the invariant ZEK on the unknot. This formula is simpler than the Wheels formula of [BGRT:WheelsWheeling], but the precise relationship between the two is yet unknown.Here's also a brief note Ami wrote a few years ago, which implies that for the Lie algebra sl(n) there are (quite simple) cubic symmetric invariant tensors. As diagrams of the kind seen in the theory of finite type invariants cannot produce cubic symmetric invariant tensors, it follows that the diagrams to tensors map cannot be onto. This result is not new, but it's still nice to have a condensed summary: S3g.pdf, S3g.ps, S3g.tex.
Daniel Moskovich's home page
arXiv:math.QA/0211223
The Gauss self-linking integral of an unframed knot is not a knot invariant, but it can be turned into an invariant by adding a correction term which requires adding extra structure to the knot. We collect the different definitions/theorems/proofs concerning this correction term, most of which are well-known (at least as folklore) and put everything together in an accessible format. We then show simply and elegantly how these approaches coincide.
Maps and Machines
In this site we study the configuration space of certain machines, all placed in the plane. Machine's configuration space is an abstract way to describe all the states the machine could take. After a short introductory to topology, we implicitly construct configuration spaces for a certain family of machines, which turn out to be, oriented surfaces of varying genus. In the third part we introduce the notion of functional linkages, which are machines who can compute polynomial functions. It can be deduced from this that to each smooth manifold M, there exists a machine with configuration space homeomorphic to a finite number of copies of M.