Dror Bar-Natan:
Research Proposal
last updated: Oct. 21, 2002
A knot is a circular piece of string placed in space, freely
allowed to move but never to cross itself. A link is much the
same, except we can place several circular pieces of string rather than
just one. A knotted trivalent graph is again similar, though now
we may solder together strings to get vertices in which the ends of up
to three open strings are attached. I will refer to these types of objects
commonly as knotted objects. The collection of all knotted
objects is quite unwieldy, and given two, it is often difficult to tell
if they are the same or not. Thus an invariant of knotted
objects is simply a function from the set of knotted objects to some
simpler set in which equality is easier to test. Of course, ``better''
invariants are valued in ``richer'' sets which allow one to read more
about the original knotted objects from the value of its invariants.
Over the last 10-12 years one such invariant  (often called ``the
Kontsevich integral'' after its first definition) attracted a lot of
attention. The invariant
(often called ``the
Kontsevich integral'' after its first definition) attracted a lot of
attention. The invariant  is valued in a certain space
is valued in a certain space
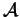 of
formal linear combinations of trivalent graphs (unknotted, plain and
easy trivalent graphs, distinct from the ones in the domain of
of
formal linear combinations of trivalent graphs (unknotted, plain and
easy trivalent graphs, distinct from the ones in the domain of  )
modulo certain relations that relate graphs that differ only in some
local way: the IHX relation
)
modulo certain relations that relate graphs that differ only in some
local way: the IHX relation
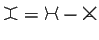 , the STU relation
, the STU relation
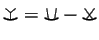 , etc. Here are some of the reasons why
, etc. Here are some of the reasons why  is so
interesting:
is so
interesting:
- There is a natural class of invariants of knotted objects, called
finite type invariants, and
 is universal in that class. In
detail: Every invariant
is universal in that class. In
detail: Every invariant 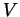 can be extended to be defined on knotted
objects that are allowed to have a finite number of self intersections
by recursively using the local formula
can be extended to be defined on knotted
objects that are allowed to have a finite number of self intersections
by recursively using the local formula
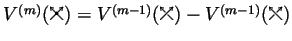 ,
where
,
where 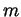 is the number of self intersections. Differences are relatives of
derivatives, and hence the extended invariant
is the number of self intersections. Differences are relatives of
derivatives, and hence the extended invariant 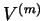 may well be thought
of as the
may well be thought
of as the 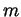 th derivative of
th derivative of 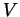 . An invariant
. An invariant 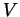 is said to be of finite
type, if, like a polynomial, one of its high derivatives
is said to be of finite
type, if, like a polynomial, one of its high derivatives 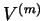 is
identically equal to 0. It turns out that
is
identically equal to 0. It turns out that  is universal in this
natural class of finite type invariants -- every finite type invariant
factors through
is universal in this
natural class of finite type invariants -- every finite type invariant
factors through  and
and  can be reconstructed given a complete knowledge
of finite type invariants. See more at [B2].
can be reconstructed given a complete knowledge
of finite type invariants. See more at [B2].
- As many of the previously known knot invariants factor through
finite type invariants it follows that invariants such as the
Alexander-Conway polynomial, the Jones polynomial, the HOMFLY and
Kauffman polynomials and Reshetikhin-Turaev invariants can all be
reconstructed from knowledge of
 . See more
at [B2].
. See more
at [B2].
- The target space
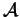 of
of  is closely related to Lie
algebras [B2]. Thus much of the rich structure
of Lie algebras can be translated to
is closely related to Lie
algebras [B2]. Thus much of the rich structure
of Lie algebras can be translated to
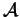 terms. This has
implications in both directions -- using tools borrowed from the
theory of Lie algebras we can learn things about
terms. This has
implications in both directions -- using tools borrowed from the
theory of Lie algebras we can learn things about
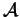 , and more
surprisingly, using knot theory we can learn some things about Lie
algebras (here I am referring for example to the recently discovered
explanation of the Harish-Chandra Duflo isomorphism of the theory of
Lie algebras in terms of a knot theoretic version of the equality
, and more
surprisingly, using knot theory we can learn some things about Lie
algebras (here I am referring for example to the recently discovered
explanation of the Harish-Chandra Duflo isomorphism of the theory of
Lie algebras in terms of a knot theoretic version of the equality
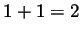 , see [BLT]).
, see [BLT]).
- The original definition of
 by Kontsevich relates
by Kontsevich relates  to the
Knizhnik-Zamolodchikov equation and hence to conformal field theory and
statistical mechanics.
to the
Knizhnik-Zamolodchikov equation and hence to conformal field theory and
statistical mechanics.
- Perhaps the nicest definition of
 is using the
Chern-Simons-Witten (CSW) path integral and Feynman
diagrams [B1]. One may attempt to compute the large
is using the
Chern-Simons-Witten (CSW) path integral and Feynman
diagrams [B1]. One may attempt to compute the large
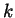 asymptotics of the latter path integral over the space of
connections
asymptotics of the latter path integral over the space of
connections 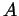 on
on
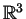 ,
using Feynman diagrams. After some repackaging, the end result is a linear
combinations of graphs such as the ones making
,
using Feynman diagrams. After some repackaging, the end result is a linear
combinations of graphs such as the ones making
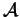 , with coefficients
given by some complicated integrals. This result is our invariant
, with coefficients
given by some complicated integrals. This result is our invariant  ,
perhaps up to some renormalization.
,
perhaps up to some renormalization.
- The hairy integrals of the previous point can be reinterpreted as
computations of degrees of certain maps of configuration spaces of
points in
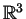 into various products of spheres (see
e.g. [BT]) and again as a beautiful discrete
counting problem of ``tinkertoy diagrams''
[T] or ``chopstick towers''
[B6].
into various products of spheres (see
e.g. [BT]) and again as a beautiful discrete
counting problem of ``tinkertoy diagrams''
[T] or ``chopstick towers''
[B6].
- There are algebraic approaches to the computation of
 : One
finds some algebraic context within which the set of knotted objects is
finitely presented using finitely many operations and finitely many generators
and relations. This done, it is now enough to specify how
: One
finds some algebraic context within which the set of knotted objects is
finitely presented using finitely many operations and finitely many generators
and relations. This done, it is now enough to specify how  should behave
under the operations and to make ``good'' guesses for the values of
should behave
under the operations and to make ``good'' guesses for the values of  on
the generators, good enough so that the relations will be satisfied.
Several such approaches exist:
on
the generators, good enough so that the relations will be satisfied.
Several such approaches exist:
- Using parenthesized tangles, the computation of
 reduces to
essentially just one guess, for the value
reduces to
essentially just one guess, for the value 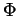 of
of  on the
associativity morphism
on the
associativity morphism
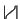 . It turns out that the required
. It turns out that the required
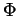 is essentially a Drinfel'd Associator, and thus its existence
(and proper behavior, in several senses) can be deduced from
Drinfel'd's work on quasi-triangular quasi-Hopf algebras.
See [LM,B3,B5].
is essentially a Drinfel'd Associator, and thus its existence
(and proper behavior, in several senses) can be deduced from
Drinfel'd's work on quasi-triangular quasi-Hopf algebras.
See [LM,B3,B5].
- Staying within the context of knotted trivalent graphs it turns out
that it is enough to guess the value of
 on the unknotted tetrahedron
on the unknotted tetrahedron
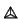 . This value turns out to be nearly equivalent to an
associator
. This value turns out to be nearly equivalent to an
associator 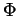 . It is also related to quantum
. It is also related to quantum 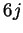 symbols for
arbitrary quantum groups.
symbols for
arbitrary quantum groups.
- There is an algebraic evaluation of
 along similar lines but
using V. Jones' [Jo] notion of planar algebras.
along similar lines but
using V. Jones' [Jo] notion of planar algebras.
- Explicit formulas for the values of
 on specific knotted objects
are surprisingly difficult to obtain. In the few cases where such
values were computed, the computations tend to be intricate but also
elegant and inspiring. See [BL,BLT].
on specific knotted objects
are surprisingly difficult to obtain. In the few cases where such
values were computed, the computations tend to be intricate but also
elegant and inspiring. See [BL,BLT].
- Finally (though only because the space is short), via a procedure
discovered by Le, Murakami and Ohtsuki [LMO]
or using the Århus integral
of [BGRT],
 can be used as
the seed for a construction of a universal finite type invariant of
3-dimensional manifolds.
can be used as
the seed for a construction of a universal finite type invariant of
3-dimensional manifolds.
Most of the picture sketched above is understood quite well, but there are
still several significant missing pieces:
- Is the invariant coming from the CSW theory precisely
equal to the
 defined using the Kontsevich integral, or is the
renormalization required really non-trivial? This is the ``vanishing of the
anomaly'' question (see [P1,P2]). I believe I can at least compute the anomaly for
a few degrees beyond what is known today, hoping that this will be enough
to resolve the question.
defined using the Kontsevich integral, or is the
renormalization required really non-trivial? This is the ``vanishing of the
anomaly'' question (see [P1,P2]). I believe I can at least compute the anomaly for
a few degrees beyond what is known today, hoping that this will be enough
to resolve the question.
- As of now, the CSW construction only works for knots
and links, but not for knotted trivalent graphs. This gap is significant
because using point 7b we should be able to
construct an associator directly from the CSW theory once it
will apply to knotted trivalent graphs as well. The problems in extending
CSW to knotted graphs are technical in nature and I hope to contribute to
their eventual solution.
- In fact, the algebraic theory of point 7b
is not yet fully written up. I hope to fix this soon.
- The relationship between point 7b and
quantum
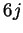 symbols is only half as good as we would like it to be --
given
symbols is only half as good as we would like it to be --
given
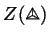 we can find appropriate solutions of the
Biedenharn-Elliot identity, but given solutions of the
Biedenharn-Elliot identity we don't know yet how to go back and find
we can find appropriate solutions of the
Biedenharn-Elliot identity, but given solutions of the
Biedenharn-Elliot identity we don't know yet how to go back and find
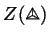 . Given a semisimple Lie algebra
. Given a semisimple Lie algebra
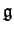 , one can
``see'' the entire quotient
, one can
``see'' the entire quotient
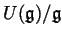 of the universal enveloping
algebra
of the universal enveloping
algebra
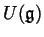 of
of
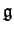 using characters of representations. What
is missing in our case is a similar theorem about a quotient like
using characters of representations. What
is missing in our case is a similar theorem about a quotient like
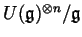 . We hope to state and prove such a theorem.
. We hope to state and prove such a theorem.
- It is known that algebraic constructions as in
point 7a are stronger than those of
point 7c, in the sense that given a construction
of the former kind it leads to a construction of the latter kind. It is not
known if this dominance is strict. If it isn't,
point 7c will become a beautiful new and natural
way of arriving at associators. If it is, it means that constructions of
the 7c kind are easier than constructions of
the 7a kind. That too would be good news for
7a requires associators and the constructions we
currently have for associators are far from easy and simple. I hope to
clarify these points in my research over the next few years.
- Last, but perhaps most important -- the picture discussed
here is too nice to be buried in hundreds of different
publications [B4], and it is time for it to be
assembled into a single integrated text. I want to write it!
The previous section may give the impression that all there is to know
about algebraic knot invariants is in the Kontsevich integral  . This
was nearly true until about two years ago, when
Khovanov [K1] proved the following
unexpected
. This
was nearly true until about two years ago, when
Khovanov [K1] proved the following
unexpected
Theorem. (sketch) Given a planar projection of a knot or
a link, there is a graded chain complex whose homology is an invariant of
the underlying knot or link and whose graded Euler characteristic is the
Jones polynomial of that knot or link.
Thus the Khovanov homology (``categorification'') relates to the Jones
polynomial like homologies relates to Euler characteristics --
potentially, it is vastly richer. (And this homology seems to have
nothing to do with  ...). In the time since Khovanov stated his
theorem, this potential seems have to become reality -- I have
shown [B7] that the Khovanov homology is
indeed stronger than the original Jones polynomial, while
Khovanov [K3] and
Jacobsson [Ja] have shown that ``maps between
knots'' (more precisely -- cobordisms between knots) induce invariant
maps between their homologies. There are indications that there are
parallel categorifications at least of the Alexander polynomial and of
the
...). In the time since Khovanov stated his
theorem, this potential seems have to become reality -- I have
shown [B7] that the Khovanov homology is
indeed stronger than the original Jones polynomial, while
Khovanov [K3] and
Jacobsson [Ja] have shown that ``maps between
knots'' (more precisely -- cobordisms between knots) induce invariant
maps between their homologies. There are indications that there are
parallel categorifications at least of the Alexander polynomial and of
the 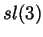 invariant of knots and links.
invariant of knots and links.
My current computer program for computing Khovanov homology is
extremely inefficient and the main reason for that is inherently
mathematical -- as it is, Khovanov's chain complex is just too big. An
indication for that is the fact that the rank of the homology is
invariably much smaller than the dimensions of the spaces of chains
involved. I believe I can do a lot better by mixing some homological
algebra and some sophisticated programming, and I hope to do so
sometime over the grant period.
The Jacobsson-Khovanov invariant of knot cobordisms was never computed for
anything. It may be of huge value, or it may be trivial. With some effort
I believe I should be able to compute this invariant on a large number of
specific cobordisms and hopefully determine its value.
Very little is known about the potential categorifications of the Alexander
polynomial and of the 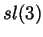 invariant. I plan to attempt to find
combinatorial constructions for these invariants and to use those
constructions for concrete computations.
invariant. I plan to attempt to find
combinatorial constructions for these invariants and to use those
constructions for concrete computations.
I am not sure if a grant proposal is the appropriate forum to come out
of the closet, but here I go. I love to write little programs that do
mathematically significant things. I've done that all along and I will
do that further on. Several of the projects mentioned above are about
such programs or will require such programs, and I have several other
such projects in mind. So I plan to invest some time to decide on the
appropriate foundations: How do I cleanly and elegantly represent
knots? Display knots? Manipulate knots? I have written programs that
do these things on an ad hoc basis, but my programs don't talk to each
other well and cannot form a consistent foundation for further
development, so I'll have to start nearly from scratch. And when the
foundations are laid, all of knot theory (and especially finite type
invariants, graph calculations as in
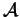 and categorification) is
there to code. I will need a big computer, students and travel money to
visit people with further ideas.
and categorification) is
there to code. I will need a big computer, students and travel money to
visit people with further ideas.
My recent progress in research activities related to the
proposal. I made significant contributions to almost every topic
discussed in this proposal. See the ``Contributions'' section of my
Form 100.
The objectives: both short and long term. As in the
``Summary for public release'' section of this proposal, my primary goals
will be to complete our understanding of the Kontsevich integral of
knotted objects and of the Khovanov categorification of certain knot
and link invariants, to make these subjects more easily accessible to
students and beginning researchers by improving their presentation, and
to compute in practice many of the theoretically computable quantities
abound in knot theory.
Literature pertinent to the proposal. See the ``References''
section of this proposal.
Methods and proposed approach. I plan to both work
analytically using the traditional mathematical
definition-theorem-proof sequence and also to use computers for a large
number of different computations.
Anticipated significance of the work. If I'll be able
to conclude my book project, it has a chance of being read by many
students and beginning researchers. Previous expositions of mine were
widely read and a book I would write may have a significant impact. I
hope my computations will also be of significance for others, as had
been the case with several computational projects I have carried out in
the past. As for the analytical research -- this is always a wild card
-- I can only hope it will lead to the eventual completion of our
understanding of the relationship between Lie algebras and knot theory
and between homological algebra and knot theory.
Training to take place through the proposal. I expect that
many parts of my proposed research will be assisted by graduate students
and postdoctoral fellows as a part of their training.
-
- B1
- D. Bar-Natan,
Perturbative aspects of the Chern-Simons topological quantum
field theory,
Ph.D. thesis, Princeton Univ., June 1991.
- B2
- D. Bar-Natan,
On the Vassiliev knot invariants,
Topology 34 (1995) 423-472.
- B3
- D. Bar-Natan,
Non-associative tangles,
in Geometric topology (proceedings of the Georgia international
topology conference), (W. H. Kazez, ed.), 139-183, Amer. Math.
Soc. and International Press, Providence, 1997.
- B4
- D. Bar-Natan,
Bibliography of Vassiliev invariants,
http://www.math.toronto.edu/~drorbn/VasBib.
- B5
- D. Bar-Natan,
On associators and the Grothendieck-Teichmuller group I,
Selecta Mathematica, New Series 4 (1998) 183-212.
- B6
- D. Bar-Natan,
From astrology to topology via Feynman diagrams and Lie algebras,
Rendiconti Del Circolo Matematico Di Palermo Serie II Suppl. 63
(2000) 11-16.
- B7
- D. Bar-Natan,
On Khovanov's categorification of the Jones polynomial,
Algebraic and Geometric Topology 2-16 (2002) 337-370.
- BGRT
-
D. Bar-Natan, S. Garoufalidis, L. Rozansky and D. P. Thurston,
The Århus integral of rational homology 3-spheres I-III,
parts I, II: Selecta Math., to appear. Also I:arXiv:q-alg/9706004,
II:arXiv:math.QA/9801049, III:arXiv:math.QA/9808013.
- BL
- D. Bar-Natan and
R. Lawrence,
A rational surgery formula for the LMO invariant,
to appear in the Israel Journal of Mathematics, arXiv:math.GT/0007045.
- BLT
- D. Bar-Natan, T. Q. T. Le
and D. P. Thurston,
Two applications of elementary knot theory to Lie algebras and
Vassiliev invariants,
Hebrew University, SUNY at Buffalo and Harvard University preprint,
April 2002, arXiv:math.QA/0204311.
- BT
- R. Bott and C. Taubes,
On the self-linking of knots,
Jour. Math. Phys. 35 (1994).
- Ja
- M. Jacobsson,
An invariant of link cobordisms from Khovanov's homology
theory,
arXiv:math.GT/0206303.
- Jo
- V. Jones,
Planar algebras, I,
University of California at Berkeley preprint, September 1999,
arXiv:math.QA/9909027.
- K1
- M. Khovanov,
A categorification of the Jones polynomial,
University of California at Davis preprint, arXiv:math.QA/9908171.
- K2
- M. Khovanov,
A functor-valued invariant of tangles,
University of California at Davis preprint, arXiv:math.QA/0103190.
- K3
- M. Khovanov,
An invariant of tangle cobordisms,
University of California at Davis preprint, arXiv:math.QA/0207264.
- LM
- T. Q. T. Le and J. Murakami,
The universal Vassiliev-Kontsevich invariant for framed
oriented links,
Compositio Math. 102 (1996), 41-64,
arXiv:hep-th/9401016.
- LMO
- T. Q. T. Le, J. Murakami and
T. Ohtsuki,
On a universal quantum invariant of 3-manifolds,
Topology 37-3 (1998) 539-574, arXiv:q-alg/9512002.
- P1
- S. Poirier,
The limit configuration space integral for tangles and the
Kontsevich integral,
Université de Grenoble I preprint, February 1999,
arXiv:math.GT/9902058.
- P2
- S. Poirier,
A note on the configuration space integral,
preprint, January 2002.
- T
- D. Thurston,
Integral expressions for the Vassiliev knot invariants,
Harvard University senior thesis, April 1995, arXiv:math.QA/9901110.
Dror Bar-Natan
2002-10-21
![]() (often called ``the
Kontsevich integral'' after its first definition) attracted a lot of
attention. The invariant
(often called ``the
Kontsevich integral'' after its first definition) attracted a lot of
attention. The invariant ![]() is valued in a certain space
is valued in a certain space
![]() of
formal linear combinations of trivalent graphs (unknotted, plain and
easy trivalent graphs, distinct from the ones in the domain of
of
formal linear combinations of trivalent graphs (unknotted, plain and
easy trivalent graphs, distinct from the ones in the domain of ![]() )
modulo certain relations that relate graphs that differ only in some
local way: the IHX relation
)
modulo certain relations that relate graphs that differ only in some
local way: the IHX relation
![]() , the STU relation
, the STU relation
![]() , etc. Here are some of the reasons why
, etc. Here are some of the reasons why ![]() is so
interesting:
is so
interesting:
![]() . This
was nearly true until about two years ago, when
Khovanov [K1] proved the following
unexpected
. This
was nearly true until about two years ago, when
Khovanov [K1] proved the following
unexpected
![]() ...). In the time since Khovanov stated his
theorem, this potential seems have to become reality -- I have
shown [B7] that the Khovanov homology is
indeed stronger than the original Jones polynomial, while
Khovanov [K3] and
Jacobsson [Ja] have shown that ``maps between
knots'' (more precisely -- cobordisms between knots) induce invariant
maps between their homologies. There are indications that there are
parallel categorifications at least of the Alexander polynomial and of
the
...). In the time since Khovanov stated his
theorem, this potential seems have to become reality -- I have
shown [B7] that the Khovanov homology is
indeed stronger than the original Jones polynomial, while
Khovanov [K3] and
Jacobsson [Ja] have shown that ``maps between
knots'' (more precisely -- cobordisms between knots) induce invariant
maps between their homologies. There are indications that there are
parallel categorifications at least of the Alexander polynomial and of
the ![]() invariant of knots and links.
invariant of knots and links.
![]() invariant. I plan to attempt to find
combinatorial constructions for these invariants and to use those
constructions for concrete computations.
invariant. I plan to attempt to find
combinatorial constructions for these invariants and to use those
constructions for concrete computations.
![]() and categorification) is
there to code. I will need a big computer, students and travel money to
visit people with further ideas.
and categorification) is
there to code. I will need a big computer, students and travel money to
visit people with further ideas.