Dror Bar-Natan:
Publications:
On Khovanov's Categorification of the Jones Polynomial
Algebraic and Geometric Topology 2-16 (2002) 337-370
first posted Sep. 2001, last updated Dec. 5, 2005
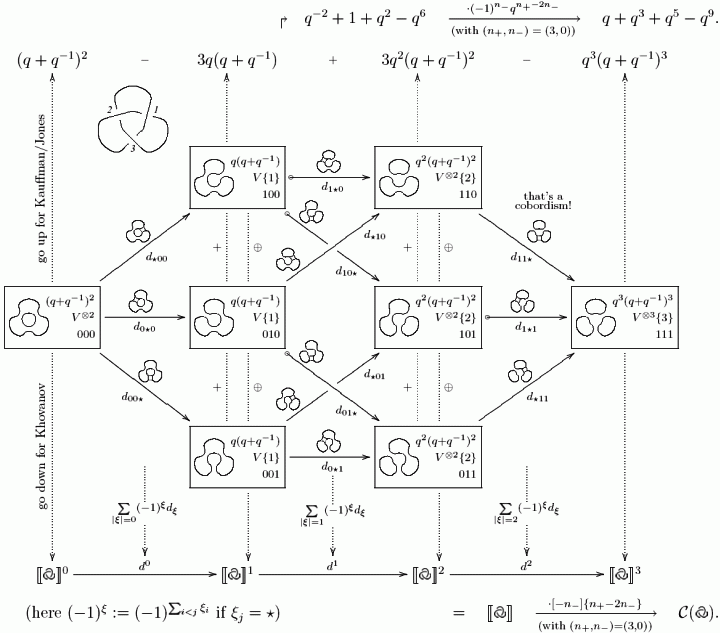
In the summer of 2001 the author of this note spent a week at Harvard
University visiting David Kazhdan and Dylan Thurston. Our hope for
the week was to understand and improve Khovanov's seminal work on
the categorification of the Jones polynomial (see arXiv:math.QA/9908171
and arXiv:math.QA/0103190).
We've hardly achieved the first goal and certainly not the second; but
we did convince ourselves that there is something very new and novel in
Khovanov's work both on the deep conceptual level (not discussed here)
and on the shallower surface level. For on the surface level Khovanov
presents invariants of links which contain and generalize the Jones
polynomial but whose construction is like nothing ever seen in knot theory
before. Not being able to really digest it we decided to just chew some,
and then provide our output as a note containing a description of his
construction, complete and consistant and accompanied by computer code
and examples but stripped of all philosophy and of all the linguistic
gymnastics that is necessary for the philosophy but isn't necessary
for the mere purpose of having a working construction. Such a note may
be more accessible than the original papers. It may lead more people to
read Khovanov at the source, and maybe somebody reading such a note will
figure out what the Khovanov invariants really are. Read on!
Based on the computations presented in the paper, several rather
strong "phenomenological" observations about Khovanov's
categorification have been made. Some are in the paper, and here are
some more:
Finally, there is a newer and more powerful program to compute
Khovanov homologies, by Alexander Shumakovitch. It's here.
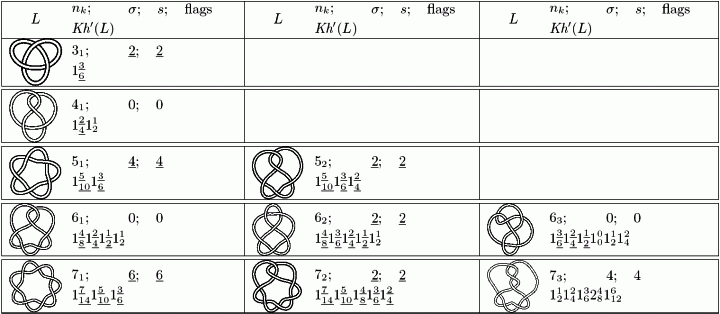
(free sample - more inside!)


