Dror Bar-Natan: Papers: Categorification:
Explaining the "Categorification.m" Program
The purpose of this document, written on September 17 2008 along with Jana Archibald, Zsuzsanna Dancso, Iva Halacheva, Louis Leung and Krzysztof Putyra is play around a bit with Dror's old "categorification.m" mathematica program, which computes Khovanov homology. Hopefully, Krzysztof will use this knowledge to produce a program to compute his variant of "odd" Khovanov homology. The original program is available at http://www.math.toronto.edu/~drorbn/papers/Categorification/Categorification.m. It is reproduced here in (mostly) red, with minor modifications to make it compliant with KnotTheory` conventions.
This Mathematica notebook is available at http://www.math.toronto.edu/~drorbn/papers/Categorification/CategorificationProgramExplained.nb.
First, let us load KnotTheory` :
In[1]:=
![]()
![]()
PD conventions are explained at http://katlas.org/wiki/Planar_Diagrams.
In[2]:=
![]()
![]()
Out[2]=
![]()
First, for degree reasons, we need to count the positive and negative crossings in pd :
In[3]:=
![]()
In[5]:=
![]()
In[6]:=
![]()
Out[6]=
![]()
In[7]:=
![]()
Out[7]=
![]()
Let' s implement the smoothing rules : X[i, j, k, l] -> either p[i, j] p[k, l] or p[i, l] p[j, k] . First. "p" must be "commutative" or ""Orderless":
In[8]:=
![]()
In[9]:=
![]()
In[10]:=
![]()
Out[10]=
![]()
We now go into the definition of "S", which stands for "Smoothing" : it gets an input which is a PD and either a list {0, 0, 1, 0} of zeros and ones or a string "0010".
In[11]:=
![]()
In[12]:=
![]()
Out[12]//FullForm=
![]()
In[13]:=
![]()
Out[13]=
![]()
In[14]:=
![]()
In[15]:=
![]()
Out[15]=
![]()
Constructing the vertices of the Khovanov cube
First, a simple variant:
In[16]:=
![]()
Out[17]=
![]()
In[18]:=
![]()
Out[18]=
![]()
In[19]:=
![]()
Out[19]=
![]()
In[20]:=
![]()
Out[21]=
![]()
In[22]:=
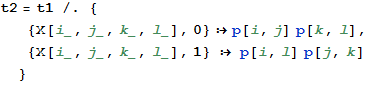
Out[22]=
![]()
In[23]:=
![]()
Out[23]=
![]()
In[24]:=
![]()
Out[24]=
![]()
In[25]:=
![]()
Out[25]=
![]()
In[26]:=
![]()
Out[26]=
![]()
In[27]:=
![]()
Out[27]=
![]()
So our smoothing has 3 cycles!
In[28]:=
![]()
Out[28]=
![]()
"p[i,j][m]" means "a path from i to j, named m; by convention, a path is named after the minimal edge inside it.
In[29]:=

In[30]:=
![]()
Out[30]=
![]()
In[31]:=
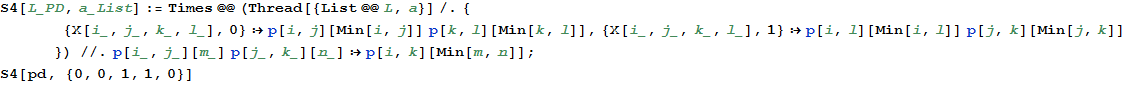
Out[32]=
![]()
In[33]:=
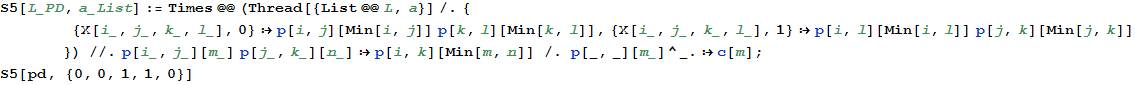
Out[34]=
![]()
In[35]:=
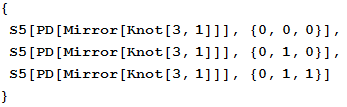
Out[35]=
![]()
Yet, we want S to also understand "*" s!
In[36]:=
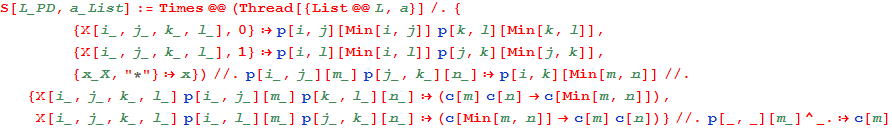
In[37]:=
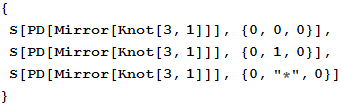
Out[37]=
![]()
In[38]:=
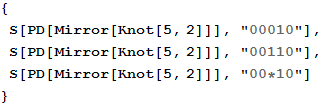
Out[38]=
![]()
In[39]:=

In[40]:=
![]()
Out[40]=
![]()
In[41]:=
![]()
Out[41]=
![]()
In[42]:=
![]()
Out[42]=
![]()
In[43]:=
![]()
Out[43]=
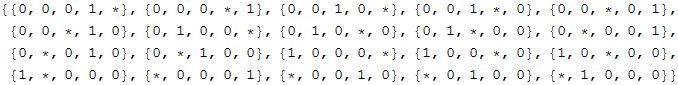
In[44]:=
![]()
Out[44]=
![]()
In[45]:=
![]()
Out[45]=
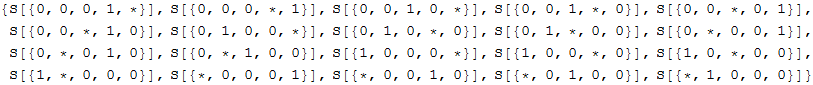
In[46]:=
![]()
Out[47]=
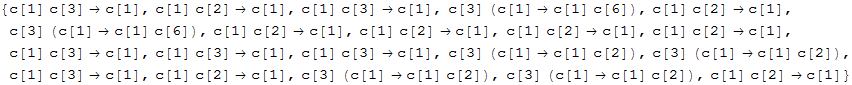
Define the degree of an arbitrary combination of v_ + and v_ - ' s :
In[48]:=
![]()
In[49]:=
![]()
Out[49]=
![]()
In[50]:=
![]()
Out[50]=
![]()
In[51]:=
![]()
Out[51]=
![]()
In[52]:=
![]()
Out[52]=
![]()
In[53]:=
![]()
Out[53]=
![]()
In[54]:=
![]()
Out[54]=
![]()
In[55]:=
![]()
Out[55]=
![]()
V[L, a] is the vector space sitting at a for L, V[L, a, deg] will be the degree deg part of V[L, a]:
In[56]:=

In[59]:=
![]()
Out[59]=
![]()
In[60]:=
![]()
Out[60]=
![]()
In[61]:=
![]()
Out[61]=
![]()
In[62]:=
![]()
Out[62]=
![]()
In[63]:=
![]()
Out[63]=
![]()
In[64]:=
![]()
Out[64]=
![]()
Defining the edge morphisms :
In[65]:=
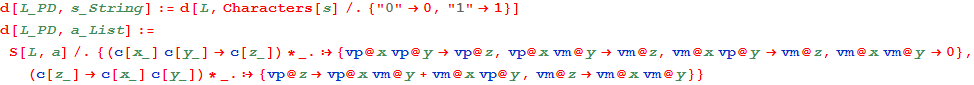
In[67]:=
![]()
Out[67]=
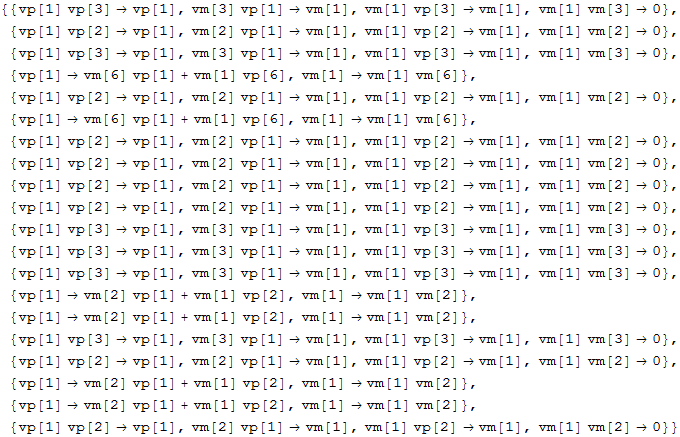
In[68]:=
![]()
Out[68]=
![]()
In[69]:=
![]()
Out[69]=
![]()
The "column" direct sums :
In[70]:=

In[72]:=
![]()
Out[72]=

The differential
In[73]:=
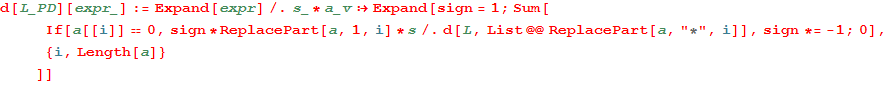
In[74]:=
![]()
Out[74]=
![]()
In[75]:=
![]()
Out[75]=
![]()
In[76]:=
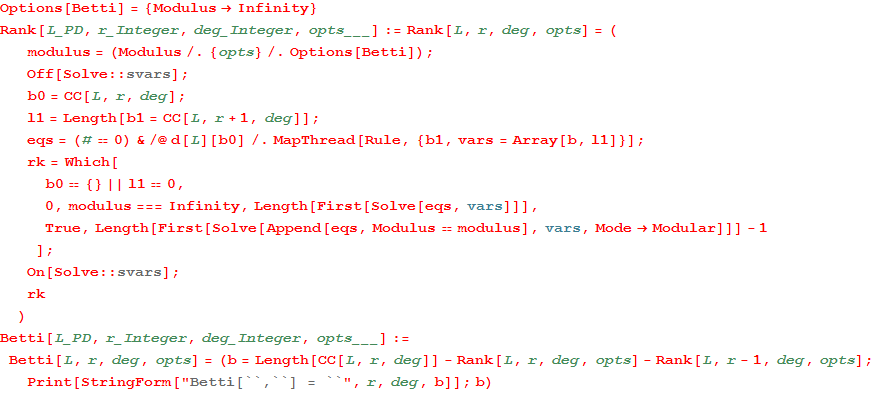
Out[76]=
![]()
In[79]:=

In[81]:=
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Out[81]=
![]()