
|
|

|
brief notes for lectures given in
Srni, January 1999
published at
Rendiconti
Del Circolo Matematico Di Palermo Serie II Suppl. 63
(2000) 11-16
Date: November 25, 1999.
Institute of Mathematics
The Hebrew University
Giv'at-Ram, Jerusalem 91904
Israel
The lecture announcements are at
http://www.math.toronto.edu/~drorbn/Talks/Srni-9901/.
This document is
http://www.math.toronto.edu/~drorbn/Talks/Srni-9901/notes.html.
A PostScript version is at
http://www.math.toronto.edu/~drorbn/Talks/Srni-9901/notes.ps.
The TeX source is at
http://www.math.toronto.edu/~drorbn/Talks/Srni-9901/notes.uu
(see directions there).
We started by viewing some pictures of Stonehenge ,

|
|

|
as well as a picture from an advertisement campaign of Andersen Consulting, a company totally unrelated to my Århus friend Jørgen Ellegaard Andersen:

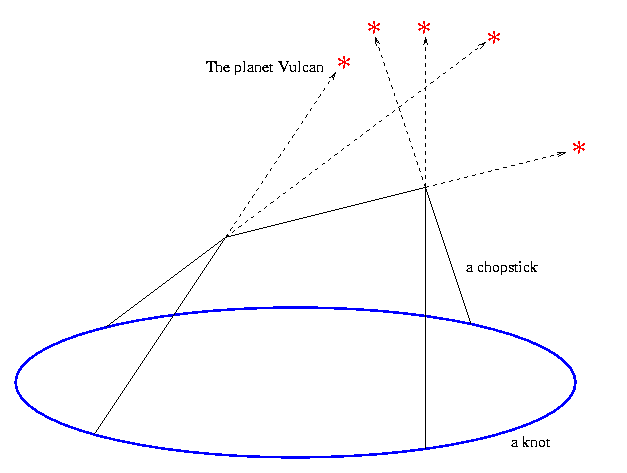
These stellar images motivated us to study stellar coincidences. We
therefore picked a knot, given as a specific embedding of ![]() in
in
![]() , and counted (with signs) the number of
``Stonehenge-inspired chopstick towers'' that can be built upon it;
namely, the number of delicate arrangements of chopsticks whose ends
are lying on the knot or are supporting each other in trivalent corners
joining three chopsticks each, so that each chopstick is pointing at a
different pre chosen point in heaven that has a high mythical meaning. One
example of such ``Stonehenge-inspired chopstick tower'' is below:
, and counted (with signs) the number of
``Stonehenge-inspired chopstick towers'' that can be built upon it;
namely, the number of delicate arrangements of chopsticks whose ends
are lying on the knot or are supporting each other in trivalent corners
joining three chopsticks each, so that each chopstick is pointing at a
different pre chosen point in heaven that has a high mythical meaning. One
example of such ``Stonehenge-inspired chopstick tower'' is below:
These ``chopstick counts'' can be all incorporated together to produce a single ``generating function'', by setting
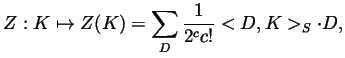
where ![]() denotes the ``Stonehenge pairing'' of a diagram
denotes the ``Stonehenge pairing'' of a diagram ![]() (that
is made of
(that
is made of ![]() chopsticks) with a given knot embedding
chopsticks) with a given knot embedding ![]() ; that is,
the (signed) number of ways a chopstick tower whose underlying
combinatorics is
; that is,
the (signed) number of ways a chopstick tower whose underlying
combinatorics is ![]() can be placed upon the specific embedding
can be placed upon the specific embedding ![]() . The
whole sum
. The
whole sum ![]() should be interpreted as living in the vector space of
infinite formal linear combinations of possible diagrams
should be interpreted as living in the vector space of
infinite formal linear combinations of possible diagrams ![]() .
.
We then argued that when the target space of ![]() is divided by
appropriate relations (the AS, IHX, and STU relations), and
is divided by
appropriate relations (the AS, IHX, and STU relations), and ![]() is
modified in a minor way to correct for problems related to framings of
is
modified in a minor way to correct for problems related to framings of
![]() , then the new
, then the new ![]() is an invariant of knots valued in some space
is an invariant of knots valued in some space
![]() of ``diagrams modulo relations''.
of ``diagrams modulo relations''.
The idea of our argument was to deform ![]() while carefully tracing what
happens to a chopstick tower built upon it. Generically, such towers
simply move along with the knot, while continuously deforming. Such
continuous deformations do not alter the combinatorics underlying the
tower, and hence
while carefully tracing what
happens to a chopstick tower built upon it. Generically, such towers
simply move along with the knot, while continuously deforming. Such
continuous deformations do not alter the combinatorics underlying the
tower, and hence ![]() does not change. But occasionally a catastrophe
occurs, and a whole tower completely disappears or is newly created. We
studied the times when such catastrophes occur, and found that towers
always appear or disappear in pairs with opposite sign (with
does not change. But occasionally a catastrophe
occurs, and a whole tower completely disappears or is newly created. We
studied the times when such catastrophes occur, and found that towers
always appear or disappear in pairs with opposite sign (with ![]() remaining fixed) or in groups of three which are IHX- or STU-related.
Hence in the quotient space by IHX and STU, the space
remaining fixed) or in groups of three which are IHX- or STU-related.
Hence in the quotient space by IHX and STU, the space ![]() , we see that
, we see that
![]() remains invariant.
remains invariant.
Literature guide: ![]() was first defined (using different
terminology) by Dylan Thurston in his Harvard undergraduate
thesis [Th]. His thesis was a
continuation and completion of the work started by Bott and Taubes
in [BT] (see
also [Bo]). The more standard language in
which
was first defined (using different
terminology) by Dylan Thurston in his Harvard undergraduate
thesis [Th]. His thesis was a
continuation and completion of the work started by Bott and Taubes
in [BT] (see
also [Bo]). The more standard language in
which ![]() is described is the language of de-Rham forms on
compactified configuration spaces; this is the language used in most
of [Th],
in [BT] and [Bo], and
in the later article by Altschuler and
Freidel [AF]. (The two languages amount
to two ways of computing the degree of a map; one by counting inverse
images of a generic point, and one by integrating the pull back of a
top form). We note that significant further progress along these lines
was made by Yang [Ya] and by
Poirier [Po1,Po2].
is described is the language of de-Rham forms on
compactified configuration spaces; this is the language used in most
of [Th],
in [BT] and [Bo], and
in the later article by Altschuler and
Freidel [AF]. (The two languages amount
to two ways of computing the degree of a map; one by counting inverse
images of a generic point, and one by integrating the pull back of a
top form). We note that significant further progress along these lines
was made by Yang [Ya] and by
Poirier [Po1,Po2].
After discussing ![]() , we moved on to talk about finite type
invariants of knots and links. The idea was to define ``a derivative'' of
a knot invariant
, we moved on to talk about finite type
invariants of knots and links. The idea was to define ``a derivative'' of
a knot invariant ![]() to be a difference of its values on two
neighboring knots (knots that differ in only one crossing), and then to
define higher order derivatives as iterated differences. Once
derivatives are around, one can talk about ``polynomials'' - invariants
whose high derivatives vanish. In the case of knots, such invariants
are called ``finite type invariants'' or ``Vassiliev invariants''.
to be a difference of its values on two
neighboring knots (knots that differ in only one crossing), and then to
define higher order derivatives as iterated differences. Once
derivatives are around, one can talk about ``polynomials'' - invariants
whose high derivatives vanish. In the case of knots, such invariants
are called ``finite type invariants'' or ``Vassiliev invariants''.
Literature guide: Vassiliev invariants were first defined by Goussarov [Go1,Go2] and Vassiliev [Va1,Va2]. A definition in the spirit of the above paragraph and much further information can be found in [B-N4], and an even closer relationship between Vassiliev invariants and polynomials is in [B-N6]. Many classical knot and link invariants are Vassiliev invariants; see [Go1,B-N2,BL,B-N4,Bi,B-N5]. An extensive bibliography of Vassiliev invariants is available on the Web.
We started by completing the discussion of finite type invariants of
knots along the lines of [B-N4], introducing
chord diagrams, weight systems and the 4T relation, the STU relation
(which is equivalent to the 4T relation), and the notion of ``a
universal Vassiliev invariant'' (of which ![]() is an example).
is an example).
We then went on trying to sooth the skeptics into quiet submission by
showing how the mystic construction of ![]() is a direct descendent of
the Chern-Simons quantum field theory (whose relation to knot theory
was first discovered by Witten [Wi]). We
started by recalling perturbation theory and Feynman diagrams. This is
of course a classical subject, and there is much written about it in
many places. Two specific places that use notation that I like
(naturally) are [B-N1]
and [Å1, Appendix]. The
latter source uses the same notation as in the lecture. Anyway, we
then went and briefly mentioned the specific way Chern-Simons theory
relates to knot theory via Feynman diagrams. More details are
in [B-N1] and
in [BS, Section 3]. It can be shown
that the integrals that arise in this way from Feynman diagrams are the
same as the Bott-Taubes configuration space
integrals [BT], and that those are the same as
our construction of
is a direct descendent of
the Chern-Simons quantum field theory (whose relation to knot theory
was first discovered by Witten [Wi]). We
started by recalling perturbation theory and Feynman diagrams. This is
of course a classical subject, and there is much written about it in
many places. Two specific places that use notation that I like
(naturally) are [B-N1]
and [Å1, Appendix]. The
latter source uses the same notation as in the lecture. Anyway, we
then went and briefly mentioned the specific way Chern-Simons theory
relates to knot theory via Feynman diagrams. More details are
in [B-N1] and
in [BS, Section 3]. It can be shown
that the integrals that arise in this way from Feynman diagrams are the
same as the Bott-Taubes configuration space
integrals [BT], and that those are the same as
our construction of ![]() (see [Th]).
(see [Th]).
This lecture was devoted to the Århus integral of Bar-Natan, Garoufalidis, Rozansky, and Thurston -- an alternative construction of the LMO invariant of 3-manifolds, in the case of rational homology spheres.
The basic idea was to adopt a ``monkey's view of algebra''. We argued
that from a monkey's perspective, the space ![]() can be viewed as if it
is the universal enveloping algebra of some Lie algebra
can be viewed as if it
is the universal enveloping algebra of some Lie algebra ![]() , and
therefore by the Poincare-Birkhoff-Witt it should be isomorphic to some
space
, and
therefore by the Poincare-Birkhoff-Witt it should be isomorphic to some
space ![]() of uni-trivalent diagrams modulo the AS and IHX relations,
which is the monkey's version of the symmetric algebra
of uni-trivalent diagrams modulo the AS and IHX relations,
which is the monkey's version of the symmetric algebra ![]() of
of ![]() .
Now people can think of
.
Now people can think of ![]() as the algebra of polynomials over
as the algebra of polynomials over
![]() , and hence monkeys are entitled to consider
, and hence monkeys are entitled to consider ![]() as some space
of ``functions''. When the values of
as some space
of ``functions''. When the values of ![]() are considered as
``functions'' in this way, it turns out that the Kirby slide move (the
main move that makes the theory of 3-manifolds a quotient of the theory
of links) acts on these ``functions'' essentially by shear
transformations. Therefore if one could compute the ``integral'' of
are considered as
``functions'' in this way, it turns out that the Kirby slide move (the
main move that makes the theory of 3-manifolds a quotient of the theory
of links) acts on these ``functions'' essentially by shear
transformations. Therefore if one could compute the ``integral'' of
![]() , it would be a 3-manifold invariant. We compute such
``integrals'' in completely combinatorial terms using a formal analog
of Feynman diagrams, and call the result ``the Århus integral'' of
a rational homology sphere.
, it would be a 3-manifold invariant. We compute such
``integrals'' in completely combinatorial terms using a formal analog
of Feynman diagrams, and call the result ``the Århus integral'' of
a rational homology sphere.
Literature guide: The ``monkey's view of algebra'' is not an official name. Nevertheless, the ``monkey PBW'' theorem is stated and proven in [B-N4, Section 5] (using a different language, of course), and the monkey's view of spaces of functions is in [Å2, Section 2]. The above philosophy is presented in detail (alas, again under a different guise) in [Å1], while the proofs that everything works even outside of the African jungles is in [Å2]. Finally, the proof that the resulting invariant is equal to the LMO invariant of [LMO] is in [Å3].
 Time for Tubby Bye Bye
Time for Tubby Bye Bye
This document was generated using the LaTeX2HTML translator Version 2K.1beta (1.49)
Copyright © 1993, 1994, 1995, 1996,
Nikos Drakos,
Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999,
Ross Moore,
Mathematics Department, Macquarie University, Sydney.
The command line arguments were:
latex2html -split 0 -no_navigation -dir notes notes.tex
The translation was initiated by Dror Bar-Natan on 2002-10-19