November 1997 Presentation Topic (continued)

Problems

Let 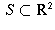be a smooth curve. Assuming uniqueness of the fronts, show that the wave fronts 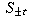defined by S at time t>0 are obtained in the following way: For 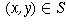, let 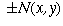be the unit normal vectors to S at the point (x,y). Then

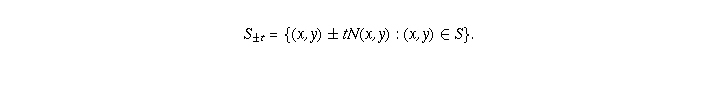
Question 2

Let 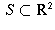be a straight line. Find 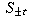for t>0.

Question 3

Let S be the parabola defined by 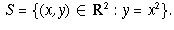Sketch the graphs of 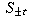for t>0. Figure 3 shows 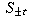for small values of t.

Question 4

Let S be the parabola defined in problem 3. Prove that the front that corresponds to the unit normal with negative y-coordinate is a smooth curve in 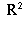for all times. Also prove that the front corresponding to the normal vector with positive y-coordinate is smooth for t small, but develops singularities for t large. Find the first value of t for which 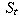has a singularity.

Question 5

Find the set of points on the plane 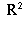which is the union of the sets of singular points of 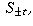t>0.

Question 6

After this discussion do you know why the cusp formed in the tea cup is brighter?

Go backward to History of the Problem
Go up to Introduction and Contents
Go forward to Some Tools to Solve the Problems
Switch to text-only version (no graphics)
Access printed version in PostScript format (requires PostScript printer)
Go to SIMMER Home Page
Go to The Fields Institute Home Page
Go to University of Toronto Mathematics Network Home Page