November 1997 Presentation Topic (continued)

History of the Problem

The particular question we are interested is the following: Given a wavefront, or the shape of a wave, at a certain time T, how do we predict the wavefront at later times t>T? Huygens' principle states that every point on any wavefront may be considered as a new source of waves, and all the points on any wavefront may be used alternatively with the source to predict any later wavefront. For simplicity we will only consider wave propagation in two dimensions. In this case we can find the wavefront at a later time by drawing a circle of radius t-T centered at each point of the wavefront at time T. The new fronts are the curves which are tangent to the all these circles.

The simplest application of Huygens' principle is when the initial front is just a point. In this case a unique circular wave is formed from that point. This can be seen, for example, when a stone is dropped on a water surface; see figure 1. In this case only one wavefront is formed. The second easiest example is the wavefront corresponding to a straight line. We can imagine the waves that are formed when a rod is dropped on a water surface. Two linear wavefronts are going to form, propagating away and in opposite directions, from the rod. This behavior is illustrated in figure 2. We also illustrate the wavefront evolution in other cases in figures 3 and 4. These pictures correspond to evolutions for short times, i.e., when t-T is small. As we can imagine, the behavior of these wavefronts for large times, except for the first and second ones, can be rather complicated. Our goal is to discuss the behavior of the fronts in figure 3 for large times.

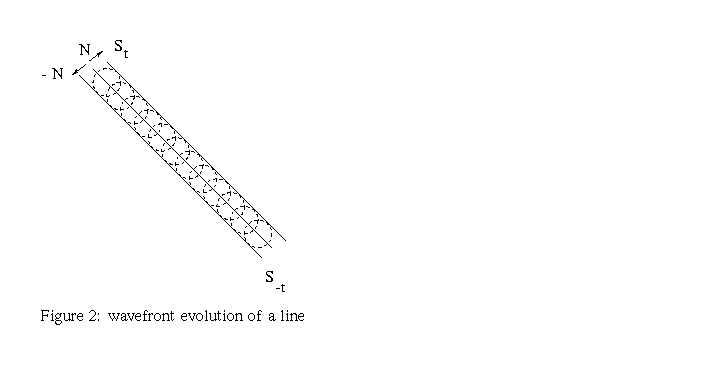
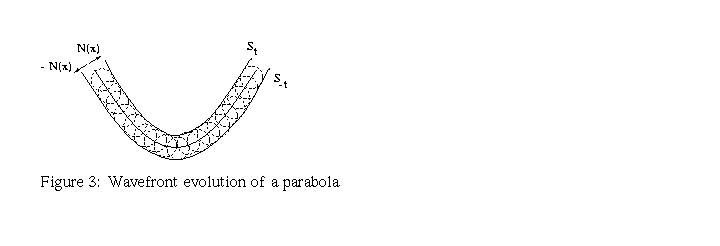
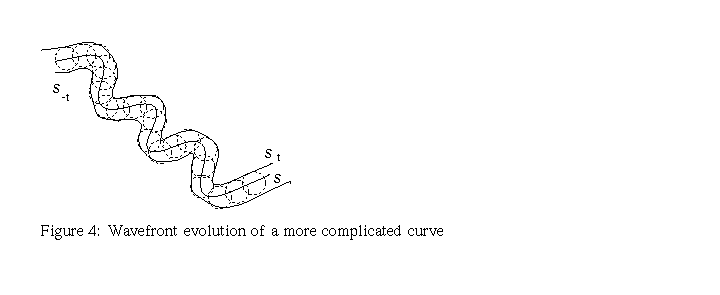
Go up to Introduction and Contents
Go forward to Problems
Switch to text-only version (no graphics)
Access printed version in PostScript format (requires PostScript printer)
Go to SIMMER Home Page
Go to The Fields Institute Home Page
Go to University of Toronto Mathematics Network Home Page