
November 1997 Presentation Topic (continued)



November 1997 Presentation Topic (continued)
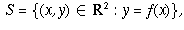 the vectors
the vectors
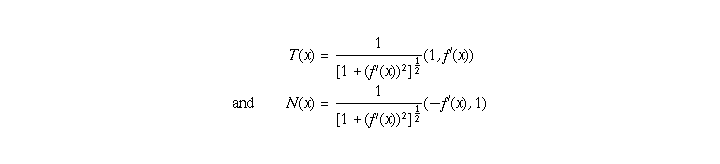
are, respectively, tangent and normal to S at the point (x,f(x)). See figure 5.
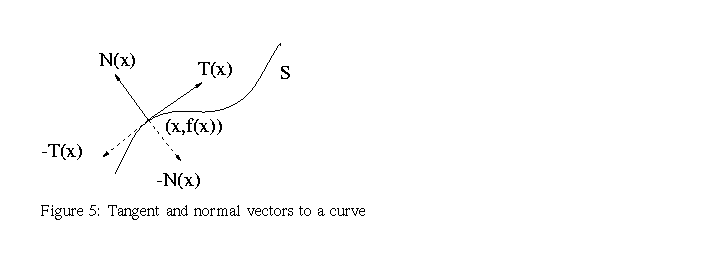
A parametrization of a curve  is a map from
an interval
is a map from
an interval 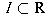 onto
onto 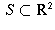 given by
given by
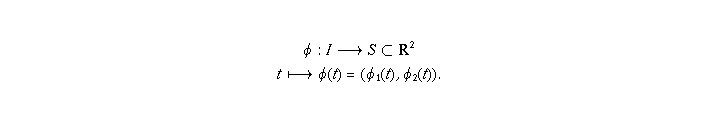
The curve S is said to be smooth at a point 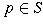 if
if
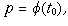
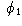 and
and 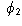 are smooth at
are smooth at 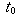 and the tangent vector
and the tangent vector
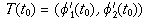 does not vanish at
does not vanish at 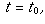 i.e.,
i.e.,
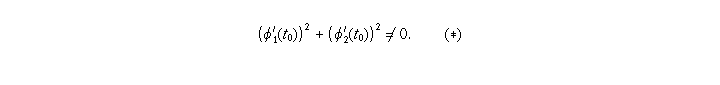
When (*) fails, the curve S has a singularity at p.
Example: The curve 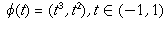 has
a singularity at
(0,0). Indeed, the tangent vector is given by
has
a singularity at
(0,0). Indeed, the tangent vector is given by
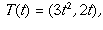 which vanishes at t=0. If we set
which vanishes at t=0. If we set 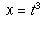 and
and
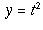 we
see that this curve is given by
we
see that this curve is given by 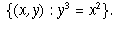 This curve is called a cubic
parabola, and this type of singularity a cusp.
The graph of this curve can be
seen in figure 6.
This curve is called a cubic
parabola, and this type of singularity a cusp.
The graph of this curve can be
seen in figure 6.
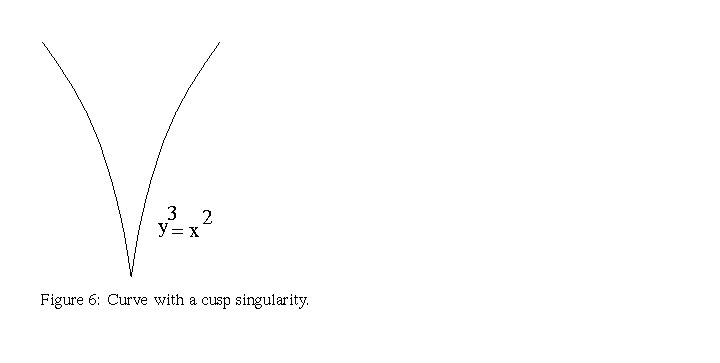


![]() Go backward to Problems
Go backward to Problems![]() Go up to Introduction and Contents
Go up to Introduction and Contents![]() Go forward to Solutions to the problems
Go forward to Solutions to the problems![]() Switch to text-only version (no graphics)
Switch to text-only version (no graphics)![]() Access printed version in PostScript format (requires PostScript printer)
Access printed version in PostScript format (requires PostScript printer) Go to SIMMER Home Page
Go to SIMMER Home Page Go to The Fields Institute Home Page
Go to The Fields Institute Home Page![]() Go to University of Toronto Mathematics Network
Home Page
Go to University of Toronto Mathematics Network
Home Page