Scalar and vector fields:

For us (there is a more general definition):

A scalar field is a function $f:S\to <!--\; \to \; -->\mathbb{R}$ and a vector field is a function $\mathbf{F}:S\to <!--\; \to \; -->{\mathbb{R}}^n$ where $S\subset <!--\; \subset \; -->{\mathbb{R}}^n$ (same dimension for the domain and the codomain!!!).

Your intuition is correct.

For instance, you can assume that you have a fluid in motion in the space, then an example of scalar field is the function giving the speed (value, for instance 25km/h) of the fluid at a point.

And an example of vector field is the function giving you the velocity (a vector, value+direction) of the fluid at a point.

Conservative vector fields:

Let $\mathbf{F}:U\to <!--\; \to \; -->{\mathbb{R}}^n$be a continuous vector field where $U\subset <!--\; \subset \; -->{\mathbb{R}}^n$is open.

The following are equivalent:

(a) The vector field $\mathbf{F}$ is a gradient field, i.e. $\mathbf{F}=\mathrm{\nabla <!--\; \nabla \; -->}f$ for some $f:U\to <!--\; \to \; -->{\mathbb{R}}^n$ a $C^1$ scalar field (we say that f is a potential of F).

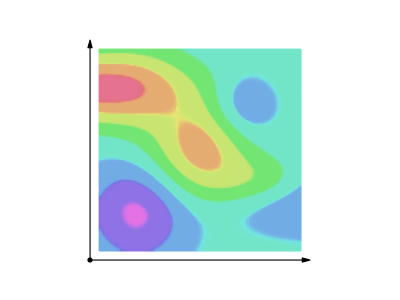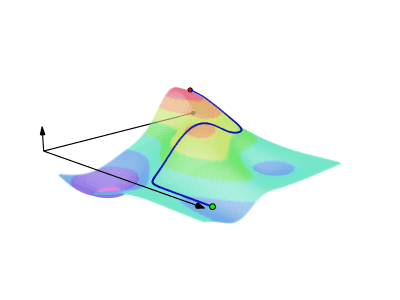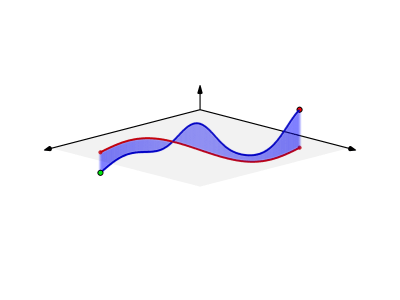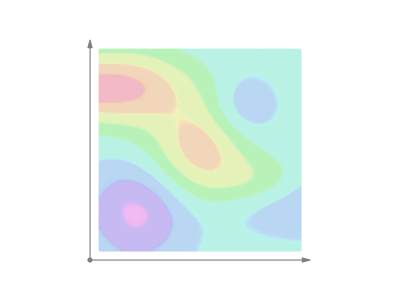
(b) The line integrals of $\mathbf{F}$ along oriented curves included in U only depend on the endpoints of the curve.

In this situation we say that $\mathbf{F}$ is conservative.

When the domain is star-shaped and $\mathbf{F}$ is $C^2$, we also have another characterization in terms of the partial derivatives (that's a special case of a general result called Poincaré Lemma): $\mathrm{\forall <!--\; \forall \; -->}i,j=1,\dots <!--\; \dots \; -->,n,\frac{\mathrm{\partial <!--\; \partial \; -->}{F}_i}{\mathrm{\partial <!--\; \partial \; -->}{x}_j}=\frac{\mathrm{\partial <!--\; \partial \; -->}{F}_j}{\mathrm{\partial <!--\; \partial \; -->}{x}_i}$

For the interpretation of (a), you can rely on your background from the first term, that's the usual gradient and you already have several geometric interpretations for it.

For instance :

1) It is the matrix representation of the differential and hence it gives the best linear approximation of f (assuming that f is differentiable, remember that being differentiable means that the tangent space exists).

2) When applying the dot-product with a vector v you get the partial derivative of f at x along v (assuming that f is differentiable).

3) It is orthogonal to the level sets (assuming that f is differentiable)

I suggest you to review the material from the first term.

http://www.math.toronto.edu/campesat/ens/1920/1010.pdf

http://www.math.toronto.edu/campesat/ens/1920/1114.pdf

For the interpretation of (b):

Line integral for scalar field:

The idea is to use the parametrization in order to "uncurve/flatten" the curve so that we get a straight segment line and then we can use the usual definition for a one variable integral.

So you should have the same intuition/interpretation for this definition and for the usual one-variable integral (draw the graph, you get some 2-dimensional surface between the curve and the graph, the integral is the area of this surface counted positively when you are above the domain or negatively when you are below, the only difference is that now the surface may be curvy).

See this animation from Wikipedia:

Line integral for vector field:

The definition is the following: you take the vector field F and you apply pointwise the dot product with the unit tangent vector so that you get a scalar field $f(\mathbf{x})=\mathbf{F}(\mathbf{x})\cdot <!--\; \cdot \; -->\mathbf{v}(\mathbf{x})$ and you compute the line integral of this scalar field (the orientation is important here to decide where is v pointing).

In practice, for a parametrization $\mathrm{\sigma <!--\; \sigma \; -->}:[a,b]\to <!--\; \to \; -->\mathbb{R}$ we get that $\mathbf{v}(\mathrm{\sigma <!--\; \sigma \; -->}(t))=\frac{{\mathrm{\sigma <!--\; \sigma \; -->}}^{\prime }(t)}{\Vert <!--\; \Vert \; -->{\mathrm{\sigma <!--\; \sigma \; -->}}^{\prime }(t)\Vert <!--\; \Vert \; -->}$ and hence (notice that the norms will cancel each other) :

${\displaystyle {\int <!--\; \int \; -->}_C\mathbf{F}\cdot <!--\; \cdot \; -->\mathrm{d}\mathbf{x}={\int <!--\; \int \; -->}_a^b\mathbf{F}(\mathrm{\sigma <!--\; \sigma \; -->}(t))\cdot <!--\; \cdot \; -->{\mathrm{\sigma <!--\; \sigma \; -->}}^{\prime }(t)\mathrm{d}t}$

1) When your vector field F is almost tangent and going to the same direction as the curve then the angle is close to 0 and you are summing the entire length of F

2) When F is almost orthogonal to the curve, the angle is close to $\pm <!--\; \pm \; -->\frac{\mathrm{\pi <!--\; \pi \; -->}}{2}$ so you are summing nothing.

3) When F is almost tangent but going in the opposite direction then the angle is close to $\mathrm{\pi <!--\; \pi \; -->}$ and you are summing the opposite of the entire length of F

I suggest you to practice the definition in order to understand the meaning of this definition and especially the dot product involved here.

For instance, I think that Q2 of this week WebWork is quite useful for that.

You can also have a look at this animation from Wikipedia:

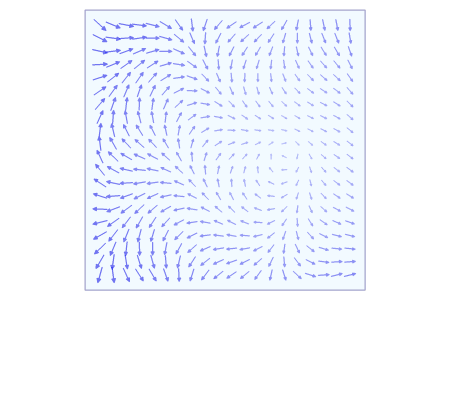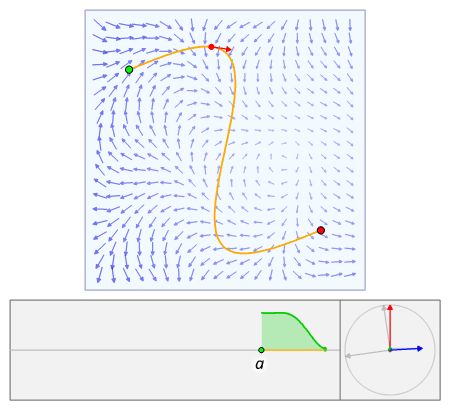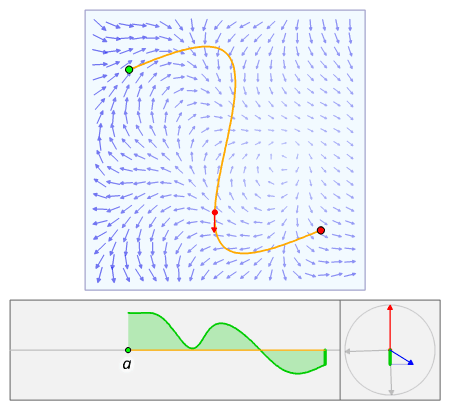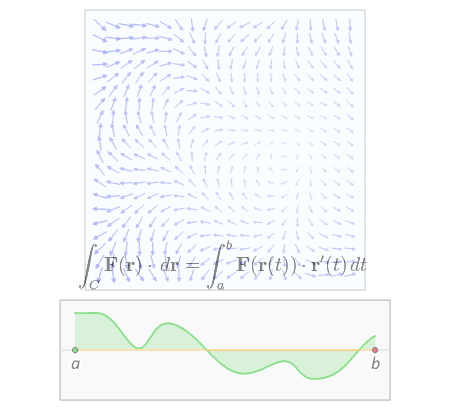
Concerning the connection between the FTC and the FTC for line integrals:

The usual FTC is just a special case of the FTC for line integrals when your curve is already a straight segment line.

Actually they are both (and also Green's theorem, Divergence Theorem, and Kelvin-Stokes theorem) a special case of a very general theorem (called Stokes theorem) from differential geometry.

See http://www.math.toronto.edu/campesat/ens/1920/stokes.pdf

Concerning the name potential:

Actually the name "potential" comes from physics.

But I think it is the same only up to a sign...

In math, we (usually) say that f is a potential for F when $\mathbf{F}=\mathrm{\nabla <!--\; \nabla \; -->}f$.

I think, that in physics, we say that f is a potential for F when $\mathbf{F}=-<!--\; -\; -->\mathrm{\nabla <!--\; \nabla \; -->}f$ (but I am not 100% sure that's always the case...)

So you have to multiply f by -1 to pass to the dark side of the Force (I let you decide whether the dark side is physics or mathematics).

For instance, the potential energy for the gravitational force is $U=-<!--\; -\; -->\frac{GMm}{\sqrt{x^2+y^2+z^2}}$

But the gravitational force is given by $\mathbf{F}=-<!--\; -\; -->\mathrm{\nabla <!--\; \nabla \; -->}U=-<!--\; -\; -->\frac{GMm}{(x^2+y^2+z^2{)}^{3/2}}(x,y,z)=-<!--\; -\; -->\frac{GMm}{r^2}\mathbf{r}$ for $\mathbf{r}=\frac{1}{\sqrt{x^2+y^2+z^2}}(x,y,z)$ and $r=\sqrt{x^2+y^2+z^2}$

By the way, if you are in physics, then the line integral corresponds to the work of the force. That may help you to have some other intuition about it.