Navigation Panel: (IMAGE)(IMAGE)(IMAGE)(IMAGE) (SWITCH TO TEXT-ONLY VERSION) (IMAGE)(IMAGE) (These buttons explained below)
UNIVERSITY OF TORONTO MATHEMATICS NETWORK

Question Corner and Discussion Area

The Case n=3 Of Fermat's Last Theorem

Asked by Tommaso Russo on August 26, 1997:
I've seen the proof for the n=4 case of Fermat's Last Theorem

Is the the n=3 case similarly easy to prove? Was the proof known by Fermat?

The proof that there are no integers X, Y, and Z which satisfy the equation (I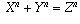MAGE) when n = 3 is similar to the proof in the case where n = 4 with the exception of a crucial lemma. The statement of the lemma is stated as follows:

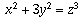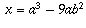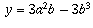If x, y, and z are integers such that (IMAGE) and x and y are relatively prime then there exist integers a and b such that (IMAGE) and (IMAGE) .

The proof of this lemma hinges on some material which is typically covered in an advanced undergraduate or an introductory graduate abstract algebra course. Those who are interested in more reading on the subject and who have enough background in mathematics can find this lemma (together with hints) as exercise 4.6 in Daniel Flath's Introduction To Number Theory (see also exercises 7.6 and 7.8 for more information on cases n=3 and n=4 of Fermat's Last Theorem).

[ Submit Your Own Question ] [ Create a Discussion Topic ]
This part of the site maintained by (No Current Maintainers)
Last updated: April 19, 1999
Original Web Site Creator / Mathematical Content Developer: Philip Spencer
Current Network Coordinator and Contact Person: Joel Chan - mathnet@math.toronto.edu

Navigation Panel: (IMAGE)(IMAGE)(IMAGE)(IMAGE) (SWITCH TO TEXT-ONLY VERSION) (IMAGE)(IMAGE)

(IMAGE) Go backward to The n=4 Case of Fermat's Last Theorem
(IMAGE) Go up to Question Corner Index
(IMAGE) Go forward to A Question from the IMO
(SWITCH TO TEXT-ONLY VERSION) Switch to text-only version (no graphics)
(IMAGE) Access printed version in PostScript format (requires PostScript printer)
(IMAGE) Go to University of Toronto Mathematics Network Home Page