Navigation Panel: (IMAGE)(IMAGE)(IMAGE)(IMAGE) (SWITCH TO TEXT-ONLY VERSION) (IMAGE)(IMAGE) (These buttons explained below)
UNIVERSITY OF TORONTO MATHEMATICS NETWORK

Question Corner and Discussion Area

A Question from the IMO

Asked by Andrew Mnih, Father Redmond High School on July 31, 1996:
I have been working on question #4 from this years IMO paper:

4. The positive integers a and b are such that the numbers 15a + 16b and 16a - 15b are both squares of positive integers. Find the least possible value that can be taken by the minimum of these two squares.

Can anyone help me solve this?

(Note: the "IMO" is the "International Mathematical Olympiad")

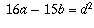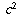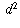The conditions given can be translated into (IMAGE) and (IMAGE) where a, b, c, and d are positive integers. You are asked to find what is the smallest that the smaller of (IMAGE) and (IMAGE) can be.

Let's try and translate all of this information into conditions on c and d. We know they have to be positive integers. The remaining conditions are that a and b have to be positive integers. So, let's solve the above system of equations to express a and b in terms of c and d.

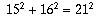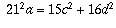If you do this, and use the fact that (IMAGE) , you get (IMAGE) . This is guaranteed to be positive, so the only other thing necessary is that a be an integer, i.e.

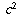(IMAGE) must be a multiple of (IMAGE) . (Condition A)
Solving for b gives (IMAGE) . This means that (IMAGE) must be greater than 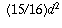(IMAGE) , and that
(IMAGE) must be a multiple of (IMAGE) . (Condition B)
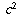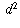Summarizing: the only conditions on the squares (IMAGE) and (IMAGE) are that they're positive, satisfy the inequality 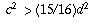(IMAGE) , and satisfy conditions A and B.

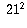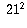Whenever you have a condition like A or B, it's useful to consider prime factors. The prime factors of (IMAGE) are 3 and 7. Let's work with 3 first. Since 3 divides (IMAGE) and 3 also divides 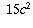(IMAGE) , condition A tells us that 3 must also divide 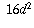(IMAGE) and hence must divide d.

Now I'm going to stop giving you the solution and see if you can work out the rest for yourself. You should be able to show that Conditions A and B together are equivalent to a very nice and simple condition on c and d, so that you can tell exactly which numbers are possible values for c and d, and hence from that determine what the smallest possible value is for one of them.

Post another message here if you get stuck further along, or if something I said here wasn't clear.

[ Submit Your Own Question ] [ Create a Discussion Topic ]
This part of the site maintained by (No Current Maintainers)
Last updated: April 19, 1999
Original Web Site Creator / Mathematical Content Developer: Philip Spencer
Current Network Coordinator and Contact Person: Joel Chan - mathnet@math.toronto.edu

Navigation Panel: (IMAGE)(IMAGE)(IMAGE)(IMAGE) (SWITCH TO TEXT-ONLY VERSION) (IMAGE)(IMAGE)

(IMAGE) Go backward to The Case n=3 Of Fermat's Last Theorem
(IMAGE) Go up to Question Corner Index
(IMAGE) Go forward to How To Find The Least Common Multiple
(SWITCH TO TEXT-ONLY VERSION) Switch to text-only version (no graphics)
(IMAGE) Access printed version in PostScript format (requires PostScript printer)
(IMAGE) Go to University of Toronto Mathematics Network Home Page