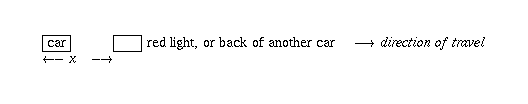






Is this model realistic? Not really; it does not take into account drivers' reaction times, limits to how fast a car can brake or accelerate, and other factors. But, although it's not completely realistic, the inadequacies of the model don't make a whole lot of difference to the basic nature of the answers you get. Working with a more realistic model requires much, much harder mathematical calculations, and the final answers aren't all that much different! So, we'll stick with this simple model.
Let's be a little more precise about how this model works. Let x denote the distance in metres between two cars (measured from the back of one to the back of another), or between the back of one car and a red light up ahead.
This is indicated below:
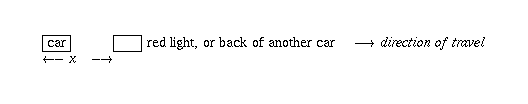
The speed v of the car is:
In the second case, l < x < L, we're assuming the car changes speed proportionally to changes in distance, so that v is given by a "linear" function of x (the graph of v as a function of x is a stratight line). This means that v = m x + b for two constants m and b. These constants can be determined from the two conditions
c, if x >= L between 0 and c, if l < x < L 0, if x <= l.
In summary, then, we're assuming that the speed of a car is given by the following function of the distance x to the closest obstacle in front of it:
where m and b can be expressed in terms of c, l, and L (which we leave for you to do). These three numbers, therefore, completely determine the traffic behaviour (according to our model).
v = c, if x >= L v = m x + b, if l < x < L v = 0, if x <= l.





