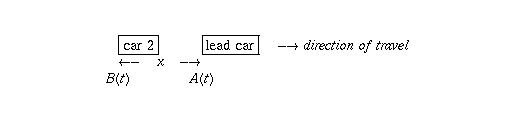






Imagine a long line of cars stopped at a red light. The light turns green. What happens?
If you've ever been near the back of such a line, you've probably sat in frustration wishing the cars in front would get a move on! But is it only their slowness in reaction?
Let's see how long it would take for the line to get moving even if everybody's reaction time is instantaneous and there's no limit on the cars' acceleration power. You may be surprised at the answer, and less inclined to blame the cars in front of you next time you're kept waiting!
So, we'll assume that, as soon as the light turns green, the lead car immediately jumps up to the speed limit c.
What happens to the car behind it? When they were stopped, the spacing between cars was l (remember, we are assuming the cars' behaviour follows the mathematical model that is described in the section Details on the Mathematical Model).
But now that the spacing has started increasing, the second car adjusts its speed proportionally to that spacing. Thus the speed v of the second car is given by an equation of the form v = m x + b, where x is the spacing and the constants m and b are determined from c, l, and L. For more details, see the section Details on the Mathematical Model.
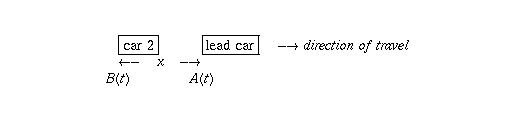
As indicated, let A(t) be the position of the lead car at time t and B(t) the position of the second car, so that x = A(t) - B(t). We want to see what sort of a function B(t) is: how the second car behaves. The easiest way to do this is to take the derivative of x: x'(t) = A'(t) - B'(t). We know that A'(t), the speed of the lead car, is just the constant c, and B'(t), the speed of the second car, is m x + b. This gives the following equation for x as a function of t:
x'(t) = c - m x(t) - bThis is probably not an equation you've learned how to solve, since it involves both the unknown function x(t) and its derivative. So, here's the way to solve it. Bring x(t) to the left-hand side and multiply both sides by
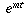 to get
to get
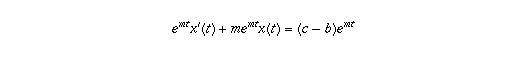
The point of multiplying by 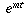 is that
now the left-hand side is the derivative of a recognizable function:
it's the derivative of
is that
now the left-hand side is the derivative of a recognizable function:
it's the derivative of 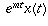 . We
therefore have
. We
therefore have
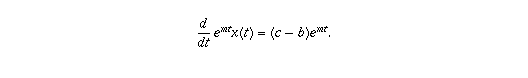
Integrate both sides to get
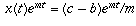 ,
then divide both sides by
,
then divide both sides by
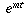 to get
to get
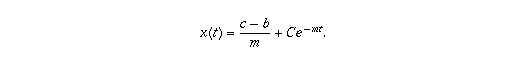
Solve for C using the fact that, at time t=0, the spacing is x(0) = l.
Now that you have a formula for x(t), you should be able to find a formula for B(t), the position of the second car. (You could have found it directly rather than going through finding x(t) first, but the integration is slightly more tedious).
Continue in this way: find formulas for the motion of the third, fourth, and subsequent cars. Much of the perceived annoyance when you're in a car is how long it takes for the traffic in front of you to start moving after a light turns green. Have you ever wished those drivers would be a little faster at accelerating? Well, here, remember, we are assuming that the cars are accelerating as fast as possible. And yet, if you correctly find the formulas, you should discover that it still takes quite a long time for the fifth or sixth car in line to get up to speed.
Try to answer the following questions: how long does it take the nth car to achieve (a) 10% of full speed, (b) 50% of full speed, (c) 90% of full speed.
You probably can't solve the whole problem exactly, but use a combination of exact formulae plus experimental evidence from the computer simulation. After following this link, read the simulation introduction if you want, then go to the "Green Light Start-Up" section and press "Start Simulation". Cars will line up at a red light at B for 120 seconds. Then the light turns green and you can watch what happens, combining this evidence with your mathematical calculations. Also try it with a non-zero value for the lead car's acceleration time, and see how much that affects things.
Additional questions to try to answer: Under our assumptions, will a car approaching a red light ever stop, or just keep moving imperceptibly slowly? Will the second and subsequent cars in line when the light turns green ever make it up to full speed c? What does this say about the realism of the assumptions we've made? And, even if our assumptions aren't completely accurate, do you think the inaccuracies are significant or minor? Finally, can you spot any "little white lies" that I have told in order to keep things simple?





