3.4 Integrability conditions or

Next: 3. The Classification Up: 3. The case of Previous: 3.3 Constancy conditions or

Subsections

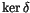
3.4 Integrability conditions or $\ker\delta$

3.4.1 +1 and -1 surgeries are opposites

3.4.2 A total twist is a composition of many little ones

**Figure 12:** Undoing a Bundle Left Twist one crossing at a time.
$\begin{figure}\begin{displaymath} \if ny \smash{\makebox[0pt]{\hspace{-0.5in} ... ...ws/UndoingBLT.tex } \hspace{-1.9mm} \end{array} \end{displaymath} \end{figure}$

**Figure 13:** The Total Twist Relation (TTR).
$\begin{figure}\begin{displaymath} \if ny \smash{\makebox[0pt]{\hspace{-0.5in} ... ...ws/TotalTwist.tex } \hspace{-1.9mm} \end{array} \end{displaymath} \end{figure}$

**Figure 14:** The Total Twist Relation (TTR).
$\begin{figure}\begin{displaymath} \if ny \smash{\makebox[0pt]{\hspace{-0.5in} ... ...put draws/TTR.tex } \hspace{-1.9mm} \end{array} \end{displaymath} \end{figure}$

3.4.3 The two ways of building an interchange

3.4.4 Lassoing a Borromean link and the IHX relation

**Figure 15:** The Monster
$\begin{figure}\begin{displaymath} \if ny \smash{\makebox[0pt]{\hspace{-0.5in} ... ...draws/Monster.tex } \hspace{-1.9mm} \end{array} \end{displaymath} \end{figure}$

**Figure 16:** Lassoing a Borromean link.
$\begin{figure}\begin{displaymath} \if ny \smash{\makebox[0pt]{\hspace{-0.5in} ... ...oingBorromean.tex } \hspace{-1.9mm} \end{array} \end{displaymath} \end{figure}$

$\begin{displaymath}{\tilde{Y}_{rab}}{Y_{rgb}}({Y_{rgp}}{Y_{pyb}}-{Y_{rgp}}-{Y_{p... ...tilde{Y}_{rab}}{Y_{rgb}}({Y_{rgp}}{\tilde{Y}_{pyb}}-{Y_{pyb}}) \end{displaymath}$

$\begin{displaymath}= {Y_{rab}}{Y_{rgb}}{Y_{rgp}}{\tilde{Y}_{pyb}} - {Y_{rab}}{Y_... ...yb}} - {Y_{rgb}}{Y_{rgp}}{\tilde{Y}_{pyb}}+{Y_{rgb}}{Y_{pyb}} \end{displaymath}$

$\begin{displaymath}= {Y_{rab}}{Y_{rgb}}{Y_{rgp}}{\tilde{Y}_{pyb}} - {Y_{rab}}{Y_... ...{Y_{rgb}}{Y_{rgp}}{\tilde{Y}_{pyb}}+{Y_{rgb}}{\tilde{Y}_{pyb}} \end{displaymath}$

(The last equality holds because in the two error terms, Y_rabY_rgb and Y_rgb, the component p is unknotted). Now reduce the component r using the total twist relation. Only the first term is affected, and 3 of the 6 terms that are produced from its reduction cancel against the 3 remaining terms of the above equation. The result is:

$\begin{displaymath}= ({Y_{rab}}{Y_{rgp}}-{Y_{rab}}-{Y_{rgp}}){\tilde{Y}_{pyb}} ... ...Y}_{rab}}{\tilde{Y}_{rgp}}{\tilde{Y}_{pyb}}-{\tilde{Y}_{pyb}}. \end{displaymath}$

The last term here drops out because in it the component r is unknotted, and so the end result is ${\tilde{Y}_{rab}}{\tilde{Y}_{rgp}}{\tilde{Y}_{pyb}}$ . In graphical terms, this is precisely the graph I! Cyclically permuting the roles of r, g, and b, we find that we have proven the IHX relation.

Next: 3. The Classification Up: 3. The case of Previous: 3.3 Constancy conditions or

Dror Bar-Natan
2000-03-19