| © | Dror Bar-Natan: Classes: 2004-05: Math 157 - Analysis I: | (52) |
Next: Homework Assignment 12
Previous: Term Exam 2 |
The results. 82 students took the exam; the average grade was 45.3 and the standard deviation was about 25.
Required thought and response. These results are disappointing. What went wrong? You are required to think about it and send me your thoughts, by email, via CCNET or using the feedback form. Did something go wrong with the way you studied? In your opinion, was the exam unfair? Did I make serious mistakes in teaching the material? Did we sink into a routine and forgot to see the bigger picture? Anything else?
The goal of this exercise is to improve things. Be constructive! Don't
just swallow or throw dirt, that won't help anyone. An indication
that ![]() went wrong is fine, but it's better if it comes along with
``and
went wrong is fine, but it's better if it comes along with
``and ![]() could have fixed it''.
could have fixed it''.
As always, anonymous messages are fine (though signed messages are better). I guess this means that I cannot verify that you all do this exercise. Yet it remains morally required, for the benefit of everybody.
The due date for this task is next Friday, December 8, at 5PM. I may or may not prepare a synopsis of your responses (with all identifying details removed) for distribution as a handout early in the next semester.
Problem 1. Let ![]() and
and ![]() be continuous functions defined
on all of
be continuous functions defined
on all of
![]() .
.
Solution. (Graded by Derek Krepski)
Problem 2. Let ![]() be a continuous function defined on
all of
be a continuous function defined on
all of
![]() , and assume that
, and assume that ![]() is rational for every
is rational for every
![]() . Prove that
. Prove that ![]() is a constant function.
is a constant function.
Solution. (Graded by Derek Krepski) Assume by contradiction that
![]() for some real numbers
for some real numbers ![]() . Between any two real numbers
there is an irrational number, so let
. Between any two real numbers
there is an irrational number, so let ![]() be some irrational number between
be some irrational number between
![]() and
and ![]() . By the intermediate value theorem there is some
. By the intermediate value theorem there is some
![]() with
with ![]() . But then
. But then ![]() is irrational, contradicting the
assumption that
is irrational, contradicting the
assumption that ![]() is rational for every
is rational for every
![]() . Thus no such pair
. Thus no such pair
![]() exists and
exists and ![]() must be a constant function.
must be a constant function.
Problem 3. We say that a function ![]() is locally
bounded on some interval
is locally
bounded on some interval ![]() if for every
if for every ![]() there is an
there is an
![]() so that
so that ![]() is bounded on
is bounded on
![]() .
Let
.
Let ![]() be a locally bounded function on the interval
be a locally bounded function on the interval ![]() and let
and let
![]() is bounded on
is bounded on ![]() and
and ![]() .
.
Solution. (Graded by Shay Fuchs)
Problem 4.
Solution. (Graded by Brian Pigott)
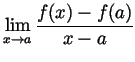 exists (and
if this limit exists, it is called
exists (and
if this limit exists, it is called 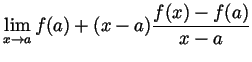 |
|||
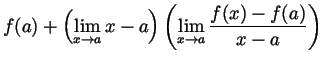 |
|||
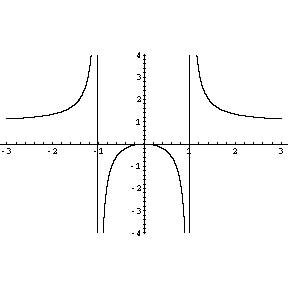
Problem 5. Draw an approximate graph of the function
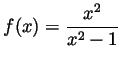 making sure to clearly indicate
(along with clear justifications) the domain of definition of
making sure to clearly indicate
(along with clear justifications) the domain of definition of ![]() , its
, its
![]() -intercepts and its
-intercepts and its ![]() -intercepts (if any), the behaviour of
-intercepts (if any), the behaviour of ![]() at
at
![]() and near points at which
and near points at which ![]() is undefined (if any),
intervals on which
is undefined (if any),
intervals on which ![]() is increasing/decreasing, its local
minima/maxima (if any) and intervals on which
is increasing/decreasing, its local
minima/maxima (if any) and intervals on which ![]() is convex/concave.
is convex/concave.
Solution. (Graded by Brian Pigott)
In summary, the graph of ![]() is roughly as follows:
is roughly as follows: