| © | Dror Bar-Natan: Classes: 2004-05: Math 157 - Analysis I: | (51) |
Next: Solution of Term Exam 2
Previous: Class Notes for Thursday November 25, 2004 |
Solve all of the following 5 problems. Each problem is worth 20 points. Write your answers in the space below the problems and on the front sides of the extra pages; use the back of the pages for scratch paper. Only work appearing on the front side of pages will be graded. Write your name and student number on each page. If you need more paper please ask the tutors. You have an hour and 50 minutes.
Allowed Material: Any calculating device that is not capable of displaying text.
Problem 1. Let ![]() and
and ![]() be continuous functions defined
on all of
be continuous functions defined
on all of
![]() .
.
Problem 2. Let ![]() be a continuous function defined on
all of
be a continuous function defined on
all of
![]() , and assume that
, and assume that ![]() is rational for every
is rational for every
![]() . Prove that
. Prove that ![]() is a constant function.
is a constant function.
Problem 3. We say that a function ![]() is locally
bounded on some interval
is locally
bounded on some interval ![]() if for every
if for every ![]() there is an
there is an
![]() so that
so that ![]() is bounded on
is bounded on
![]() .
Let
.
Let ![]() be a locally bounded function on the interval
be a locally bounded function on the interval ![]() and let
and let
![]() is bounded on
is bounded on ![]() and
and ![]() .
.
Problem 4.
Problem 5. Draw an approximate graph of the function
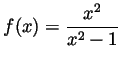 making sure to clearly indicate
(along with clear justifications) the domain of definition of
making sure to clearly indicate
(along with clear justifications) the domain of definition of ![]() , its
, its
![]() -intercepts and its
-intercepts and its ![]() -intercepts (if any), the behaviour of
-intercepts (if any), the behaviour of ![]() at
at
![]() and near points at which
and near points at which ![]() is undefined (if any),
intervals on which
is undefined (if any),
intervals on which ![]() is increasing/decreasing, its local
minima/maxima (if any) and intervals on which
is increasing/decreasing, its local
minima/maxima (if any) and intervals on which ![]() is convex/concave.
is convex/concave.