- Use
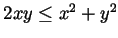 (why is this true?), with
(why is this true?), with
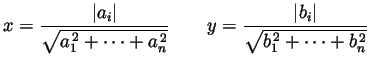
- Consider the expression
collect terms, and apply the result of Problem 1.
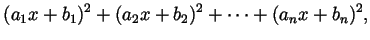
| © | Dror Bar-Natan: Classes: 2004-05: Math 157 - Analysis I: | (10) |
Next: Class Notes for Tuesday September 21, 2004
Previous: Class Notes for Thursday September 16, 2004 |
Required reading. Like last week, read, reread and rereread your notes from this week's classes, and make sure that you really, really really, really really really understand everything in them. Do the same every week! Also, read all of Spivak's Chapter 1.
To be handed in. From Spivak Chapter 1: 11 odd parts, 12 odd parts, 14, and also
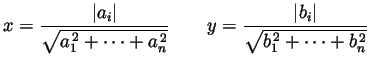
Recommended for extra practice. From Spivak Chapter 1: 7, 15, 18, 20, 21, 22, 23.
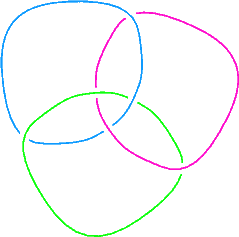
Just for fun. Can you draw 3 linked circles, with the property that if any one of them disappears, the other two are no longer linked? Can you draw 4 linked circles, with the property that if any one of them disappears, the other 3 are no longer linked? What about more than 4? (In the example below, if you drop any of the components the other two remain linked).