Homework Assignment 5
Assigned Thursday October 16; due Thursday October 23 in class.
Required reading. Sections 1 and 2 of my paper
On the Vassiliev Knot
Invariants.
To be handed in.
- Let
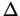 be the ``doubling'' (also called ``cabling'') operation
on knots, which takes a framed knot and replaces it by a 2-component
link by ``replacing every line by a double line'' in an obvious manner.
be the ``doubling'' (also called ``cabling'') operation
on knots, which takes a framed knot and replaces it by a 2-component
link by ``replacing every line by a double line'' in an obvious manner.
- Show that if
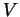 is a type
is a type 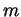 invariant of 2-component links then
invariant of 2-component links then
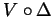 is a type
is a type 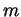 invariant of knots.
invariant of knots.
- Find a map
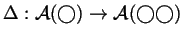 (sorry for the ``operator overloading'') for which
(sorry for the ``operator overloading'') for which
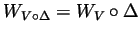 for all such
for all such 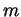 and
and 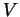 . (Verify that
you proposed map respects the
. (Verify that
you proposed map respects the 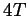 relation!)
relation!)
- If
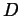 is a chord diagram, let
is a chord diagram, let 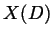 be the number of ``chord
crossings'' in
be the number of ``chord
crossings'' in 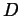 (so for example,
(so for example,
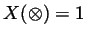 ).
).
- Does
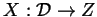 satisfy the
satisfy the 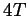 relation?
relation?
- Let
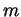 by a natural number. Can you find a type
by a natural number. Can you find a type 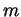 knot invariant
knot invariant
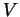 for which
for which 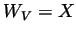 ?
?
Idea for a good deed. Tell us about the
Milnor-Moore theorem: A connected commutative and co-commutative graded
Hopf algebra over a field of characteristic 0 which is of finite
type, is the symmetric algebra over the vector space of its
primitives.
The generation of this document was assisted by
LATEX2HTML.
Dror Bar-Natan
2003-10-15
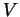 is a type
is a type 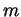 invariant of 2-component links then
invariant of 2-component links then
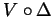 is a type
is a type 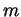 invariant of knots.
invariant of knots.
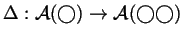 (sorry for the ``operator overloading'') for which
(sorry for the ``operator overloading'') for which
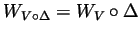 for all such
for all such  and
and  . (Verify that
you proposed map respects the
. (Verify that
you proposed map respects the 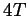 relation!)
relation!)
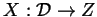 satisfy the
satisfy the 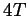 relation?
relation?
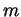 by a natural number. Can you find a type
by a natural number. Can you find a type 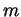 knot invariant
knot invariant
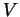 for which
for which 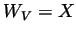 ?
?