Dror Bar-Natan: Classes: 2003-04: Math 157 - Analysis I:

(75)

Next: Homework Assignment 19 Previous: Term Exam 3

Solution of Term Exam 3

this document in PDF: Solution.pdf

Problem 1. In a very condensed form, the definition of integration is as follows: For $f$ bounded on $[a,b]$ and $P: a=t_0<t_1<\dots<t_n=b$ a partition of $[a,b]$ set $m_i=\inf_{[t_{i-1},t_i]}f(x)$, $M_i=\sup_{[t_{i-1},t_i]}f(x)$, $L(f,P)=\sum_{i=1}^n m_i(t_i-t_{i-1})$ and $U(f,P)=\sum_{i=1}^n M_i(t_i-t_{i-1})$. Then set $L(f)=\sup_P L(f,P)$ and $U(f)=\inf_P U(f,P)$. Finally, if $U(f)=L(f)$ we say that ``$f$ is integrable on $[a,b]$'' and set $\int_a^b f=\int_a^b f(x)dx=U(f)=L(f)$.

From this definition alone, without using anything proven in class about integration, prove that the function $f$ given below is integrable on $[-1,1]$ and compute its integral $\int_{-1}^1f$:

$$f(x)=\begin{cases}0 & x\neq 0 1 & x=0. \end{cases}$$

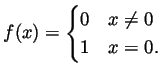
Solution. (Graded by Cristian Ivanescu) Let $P:-1=t_0<t_1<\dots<t_n=1$ be an arbitrary partition of $[-1,1]$. Then for any $i$ the infimum $m_i=\inf_{[t_{i-1},t_i]}f(x)$ is 0 and so $L(f,P)=\sum_{i=1}^n m_i(t_i-t_{i-1})=0$. Thus $L(f)=\sup_P L(f,P)=0$. At the same time, for any $i$ the supremum $M_i=\sup_{[t_{i-1},t_i]}f(x)$ is $\geq 0$, and hence $U(f,P)=\sum_{i=1}^n M_i(t_i-t_{i-1})\geq 0$ and so $U(f)=\inf_P U(f,P)\geq 0$. Now let $0<\epsilon<1$ be given and let $P_\epsilon$ be the partition $-1=t_0<t_1=-\frac{\epsilon}{2}<\frac{\epsilon}{2}=t_2<1=t_3$. Then $M_1=M_3=0$ while $M_2=1$ and so $U(f,P_\epsilon) = 0(1-\frac{\epsilon}{2}) + 1(\frac{\epsilon}{2} + \frac{\epsilon}{2}) + 0(1-\frac{\epsilon}{2})=\epsilon$. Thus $U(f)=\inf_P U(f,P)\leq\epsilon$. But this is true for any $0<\epsilon<1$ and we already know that $U(f)\geq 0$. So it must be that $U(f)=0$. Thus $U(f)=L(f)=0$ and hence $f$ is integrable on $[-1,1]$ and its integral is $\int_{-1}^1 f=U(f)=L(f)=0$.

Problem 2. Prove that the function

$$g(x):=\int_0^x\frac{dt}{1+t^2} + \int_0^{1/x}\frac{dt}{1+t^2}$$

is a constant function.

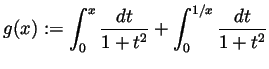
Solution. (Graded by Julian C.-N. Hung) Differentiate $g$ using the first fundamental theorem of calculus. The first summand yields $\frac{1}{1+x^2}$. The second summand is the first summand pre-composed with the function $x\mapsto 1/x$. So by the chain rule, the derivative of the second summand is $\frac{1}{1+(1/x)^2}(1/x)'=-\frac{1}{1+(1/x)^2}(1/x^2)=-\frac{1}{1+x^2}$. $g'$ is the sum of these two terms, $g'=\frac{1}{1+x^2}-\frac{1}{1+x^2}=0$. Hence $g$ is a constant.

Problem 3. In class we have proven that a twice-differentiable function $f$ satisfying the equation $f''=-f$ is determined by $f(0)$ and $f'(0)$. Use this fact and the known formulas for the derivatives of $\cos x$ and $\sin x$ to derive a formula for $\cos(\alpha+\beta)$ in terms of $\cos\alpha$, $\cos\beta$, $\sin\alpha$ and $\sin\beta$.

Solution. (Graded by Julian C.-N. Hung) Let $\beta$ be a constant and consider the functions $f_1(\alpha)=\cos(\alpha+\beta)$ and $f_2(\alpha)=\cos\alpha\cos\beta - \sin\alpha\sin\beta$. Then $f_1'' = (\cos(\alpha+\beta))'' = (-\sin(\alpha+\beta))' = -\cos(\alpha+\beta)=-f_1$ and $f_2''=(\cos\alpha\cos\beta - \sin\alpha\sin\beta)'' = (-\sin\alpha\cos\beta-\cos\alpha\sin\beta)' = -\cos\alpha\cos\beta + \sin\alpha\sin\beta=-f_2$ so both $f_1$ and $f_2$ satisfy $f''=-f$. We also have $f_1(0)=\cos\beta=\cos 0\cos\beta-\sin 0\sin\beta=f_2(0)$ and $f'_1(0)=-\sin\beta=(-\sin 0)\cos\beta-\cos 0\sin\beta=f_2'(0)$. So by what we have proven in class $f_1=f_2$ or $\cos(\alpha+\beta)=\cos\alpha\cos\beta - \sin\alpha\sin\beta$.

Problem 4. The function $F$ is defined by $F(x):=x^x$.

1. Compute $F'(x)$ for all $x>0$.
2. Explain why $F(x)$ has a differentiable inverse for $x>\frac{1}{e}$.
3. Let $S$ be the inverse function of $F$ (with the domain of $F$ considered to be $(\frac{1}{e},\infty)$). Compute $S'(x)$ and simplify your result as much as you can. Your end result may still contain $S(x)$ in it, but not $S'$, $F$ or $F'$.

Solution. (Graded by Vicentiu Tipu)

1. $$F'(x) = \left(e^{x\log x}\right)' = e^{x\log x}\left(\log x+x\frac{1}{x}\right)=x^x(1+\log x) = F(x)(1+\log x)$$.
2. For $x>\frac{1}{e}$ we have that $\log x>\log\frac{1}{e}=-1$ and hence $1+\log x>0$ and $F'(x)>0$. So $F$ is increasing on $(\frac{1}{e},\infty)$. It is also differentiable on that interval, so by a theorem proven in class, it has a differentiable inverse.
3. $$S'(x)=\frac{1}{F'(S(x))} = \frac{1}{F(S(x))(1+\log S(x))} = \frac{1}{x(1+\log S(x))}$$.

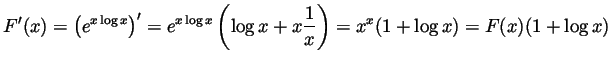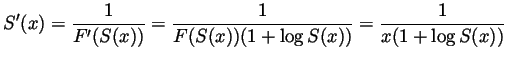The results. 82 students took the exam; the average grade was 69.3, the median was 78 and the standard deviation was 26.76.

The generation of this document was assisted by L^ATEX2HTML.