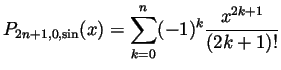 should approach
should approach
| Dror Bar-Natan: Classes: 2003-04: Math 157 - Analysis I: | (84) |
Next: Brook Taylor
Previous: Class Notes for Thursday February 26, 2004 |
Required reading. Spivak's Chapter 20.
To be handed in. From Spivak Chapter 20: Odd parts of 1, 3, 4, 8.
Recommended for extra practice. From Spivak Chapter 20: Even parts of 1, 3, 4, 8 and all of 6, 9.
Just for fun. According to your trustworthy
professor,
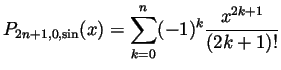 should approach
should approach ![]() when
when ![]() goes to infinity. Here are the first few
values of
goes to infinity. Here are the first few
values of
![]() :
:
|
|
|
| 0 | 157.0 |
| 1 | -644825.1666 |
| 2 | 794263446.1416 |
| 3 | -465722259874.7894 |
| 4 | 159244913619814.5429 |
| 5 | -35629004757275297.7787 |
| 6 | 5619143855101017161.3172 |
| 7 | -658116552443218272478.0047 |
| 8 | 59490490719826164706638.3418 |
| 9 | -4275606060900548165855463.4918 |
| 10 | 250142953226934230105633222.4574 |
| 100 |
|
In widths of hydrogen atoms that last value is way more than the
diameter of the observable universe. Yet surely you remember that
![]() ; in fact, my computer tells me that
; in fact, my computer tells me that ![]() is
approximately -0.0795485. In the light of that and in the light of the
above table, do you still trust your professor?
is
approximately -0.0795485. In the light of that and in the light of the
above table, do you still trust your professor?
The Small Print. For
![]() we get
we get
![]() .
.