
 |
ABOUT MEI am now an assistant professor in the Math and Statistics Department at the University of Guelph working in the area of probability, stochastic processes, and their applications to machine learning. I am also affiliated with the CARE-AI institute. Before that, I was an NSERC postdoctoral fellow at the University of Toronto. My supervisor was Jeremy Quastel. Before that, I was a PhD student at the Courant Institute of Mathematical Sciences in New York under the advisement of Gérard Ben Arous. You can reach me at: nicam + at symbol + uoguelph.ca You can find my CV by clicking here |
 UNIVERSITY OF WATERLOO
UNIVERSITY OF WATERLOO
BMath
Pure & Applied Math w/Physics Option
 NEW YORK UNIVERSITY
NEW YORK UNIVERSITY
PhD
Courant Institute of Mathematical Sciences
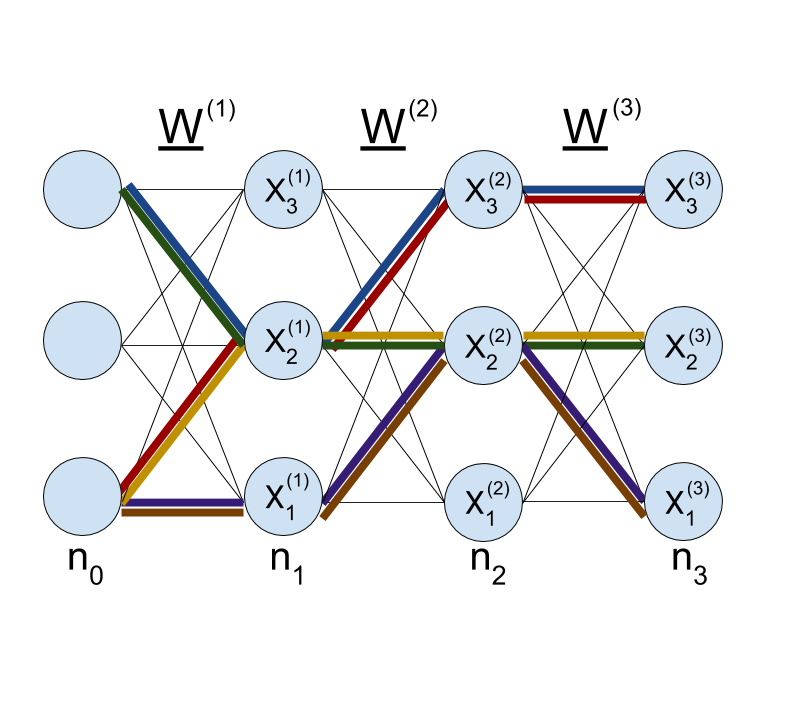
(With Boris Hanin) We prove the precise scaling, at finite depth and width, for the mean and variance of the neural tangent kernel (NTK) in a randomly initialized ReLU network.
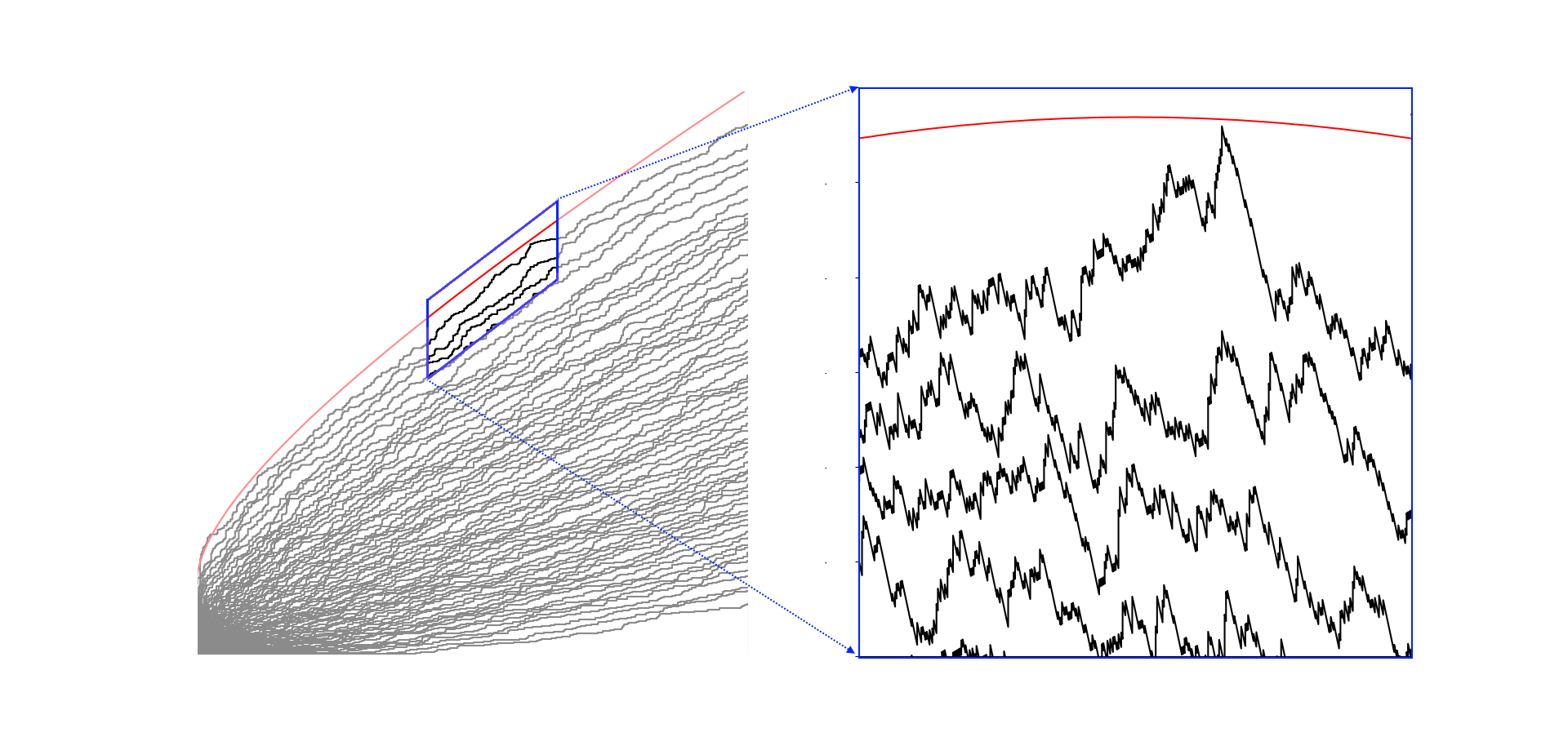
(With Duncan Dauvergne and Bálint Virág) We prove a general theorem for uniform convergence to the Airy line ensemble that applies to many different last passage percolation settings.
(With Jeremy Quastel and Daniel Remenik) We provide a direct and elementary proof for the transition probability formula for TASEP probabilities for general (one-sided) initial data solves the Kolmogorov backward equation. The same method yields the solution for the related PushASEP particle system.
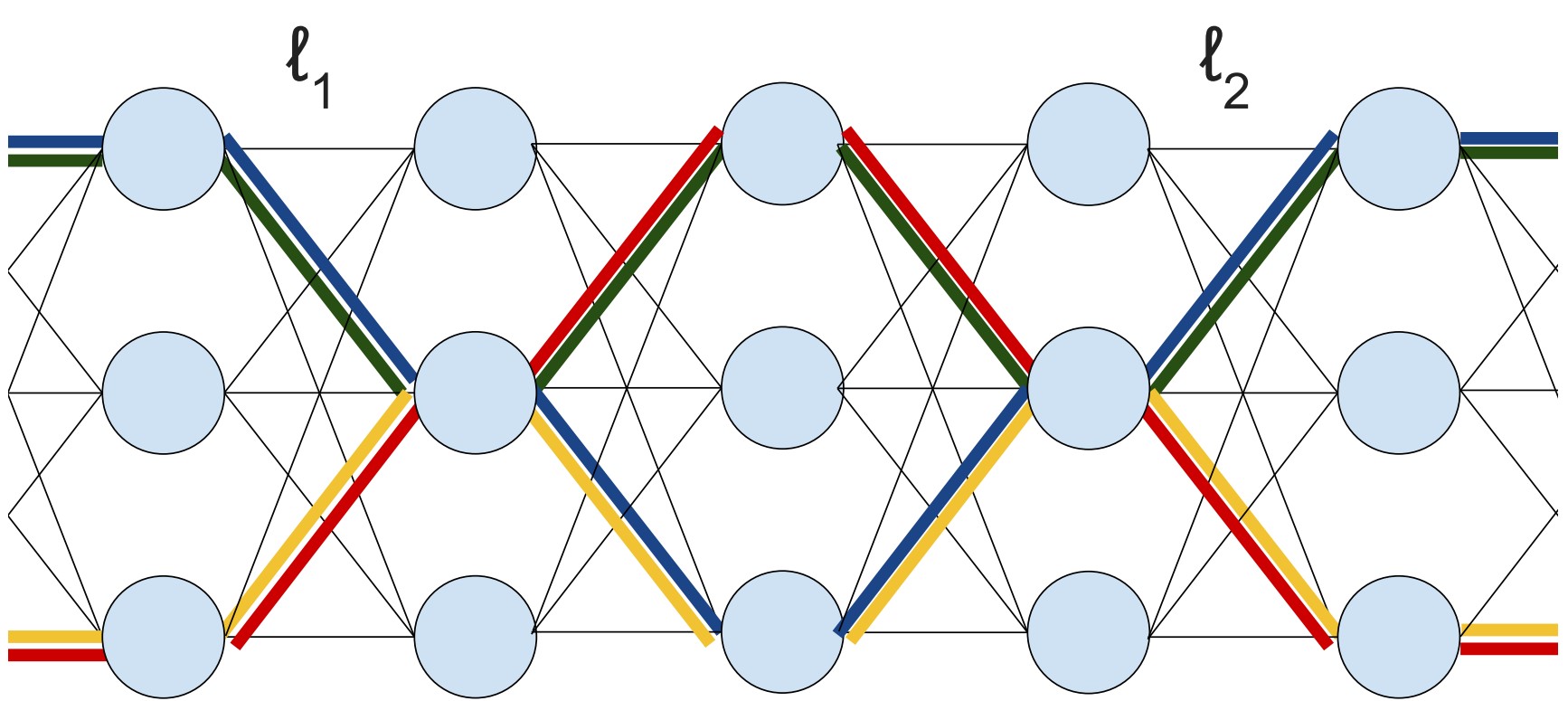
(With Boris Hanin) In this project, we prove a central-limit-type theorem for products of many random matrices. This result was motivated by deep neural nets, and provides a quantitative explanation for the vanishing and exploding gradient problem in deep neural networks. Slides available here .
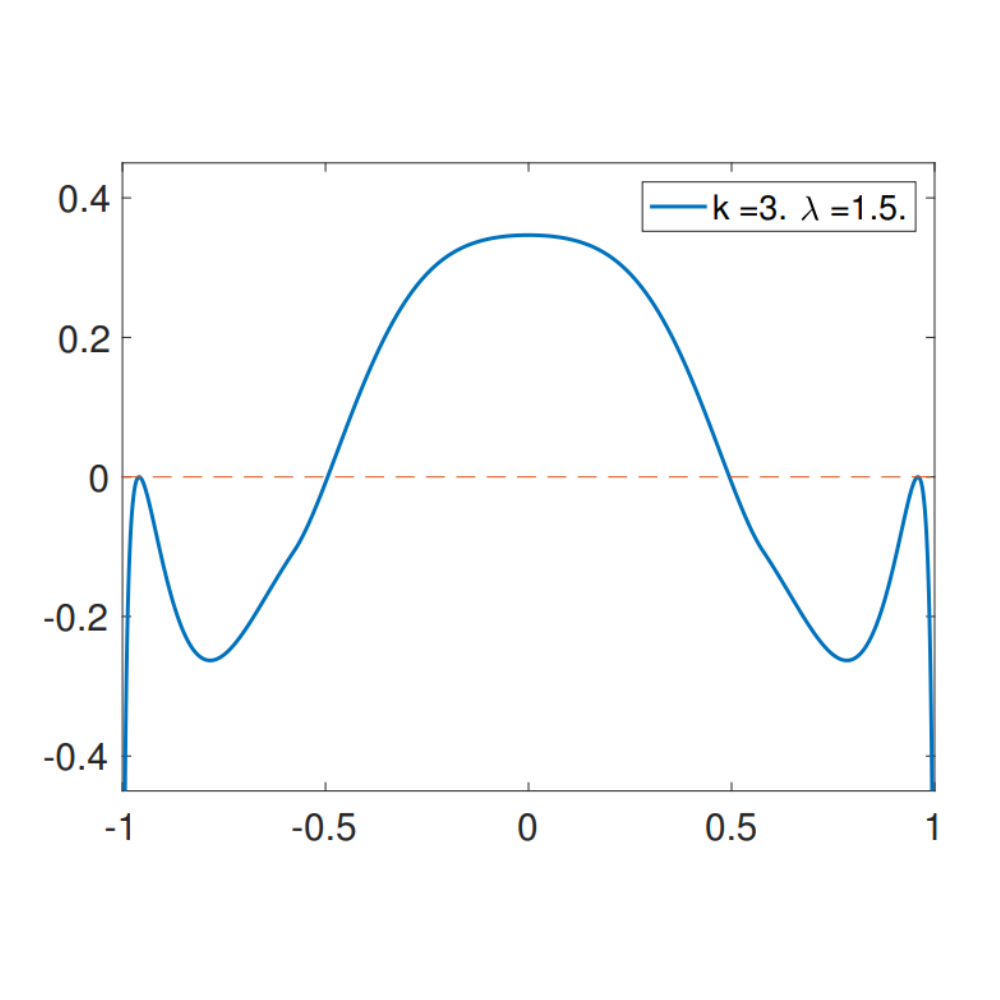
(With Gerard Ben Arous, Song Mei, Andrea Montanari) In this project we study the energy landscape of a certain random function on the N dimensional hyper-sphere. This energy landscape is a natural model for certain problems in machine learning. We find a certain critical signal-to-noise ratio in this problem below which it becomes infeasable to detect the original signal. Slides available here .
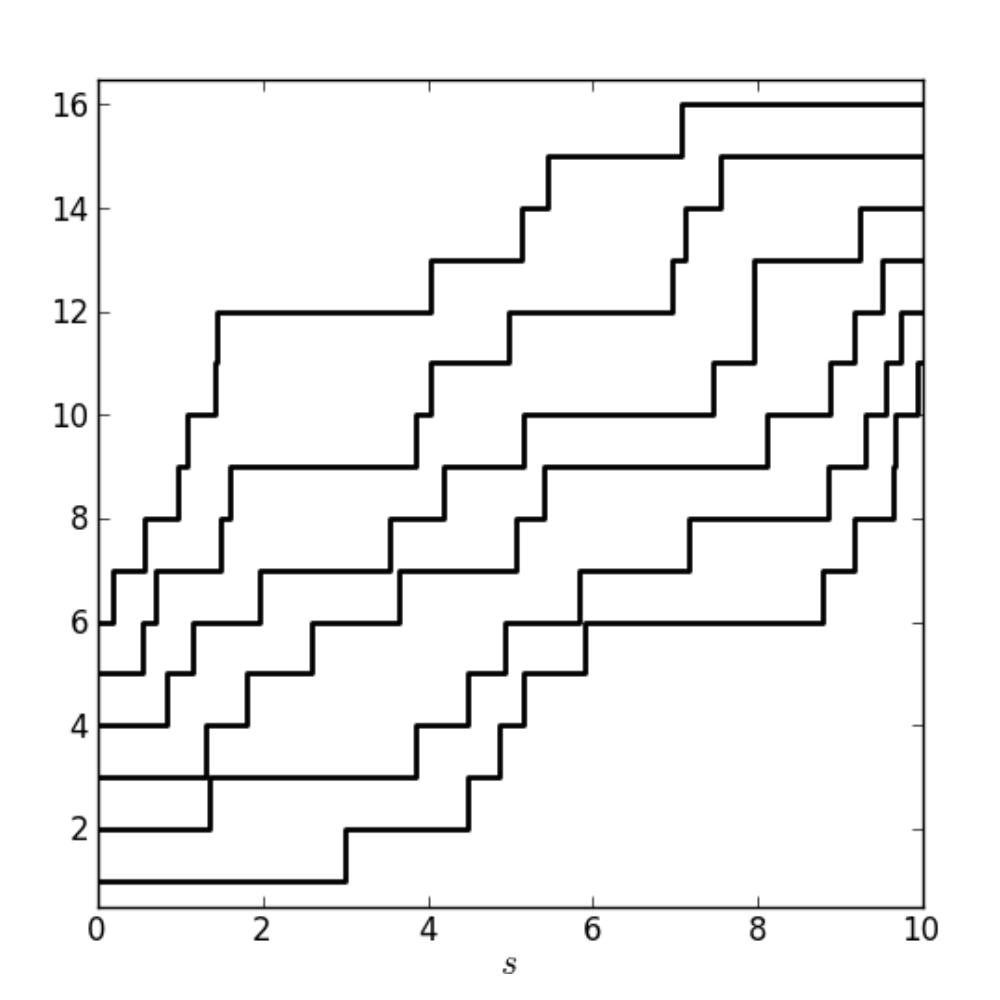
I show convergence for semi-discrete directed polymers (also known as the O'Connell-Yor polymer) to the corresponding partition function for multi-layer continuum polymers. This convergence verifies, modulo a previously hidden constant, an outstanding conjecture proposed by Corwin and Hammond in their construction of the KPZ line ensemble.
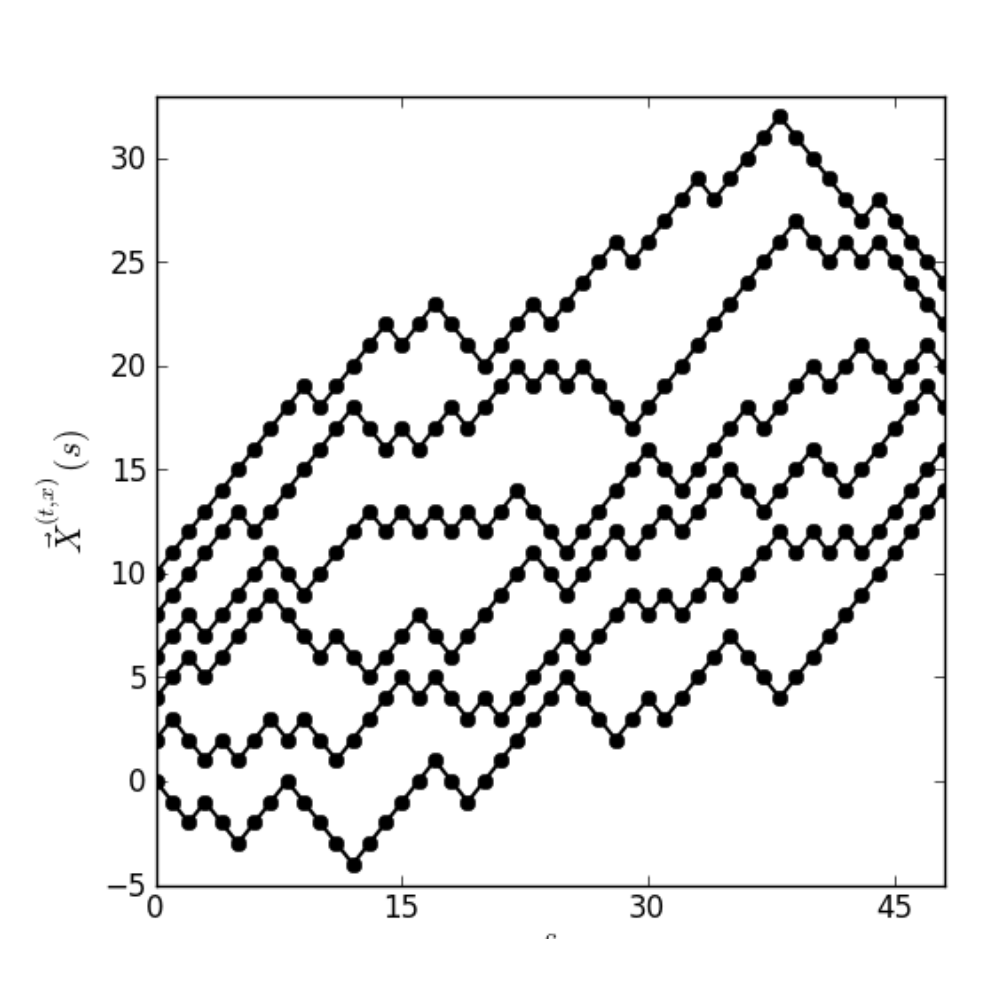
(With Ivan Corwin) A research project about the scaling limits of multiple non-intersecting directed polymers. We study the partition function of several non-intersecting walks in a random environment in the limit where the 1) the length of the walks goes to infinity 2) the randomness in the disorder goes to zero. If the rate of these two limits is tuned correctly, there is a non-trivial limit. The limit turns out to be related to the "multi-layer extension" of the stochastic heat equation. This whole construction can also be thought of as a limit for the geometric RSK process.
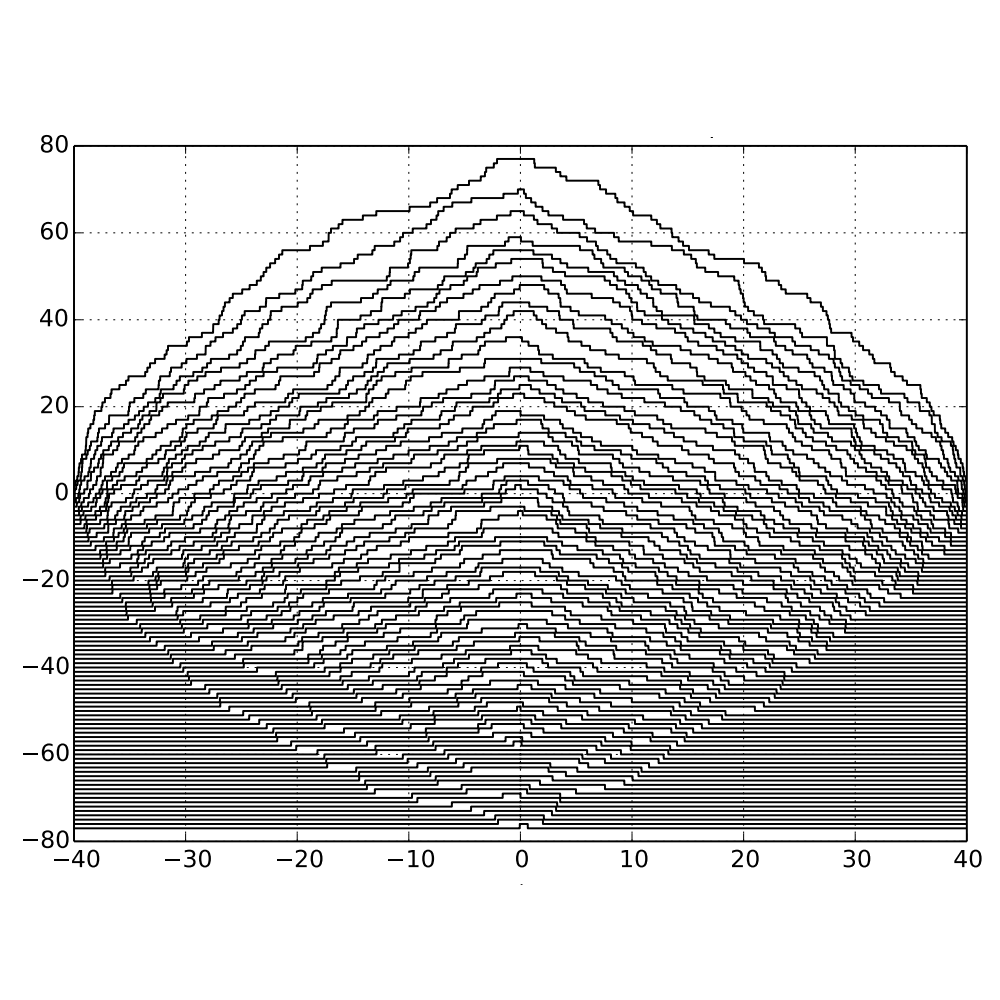
In this project, I generalized the definition of a Young Tableau to include real entries. By applying a generalization of the RS algorithm to a Poisson point process, we get a pair of random such generalized Tableau whose law is related to Schur processes and non-crossing Poisson walks. Published in Stochastic Processes and their Applications.
"Guess Who?" is a popular two player game where players ask "Yes" or "No" questions to search for their opponent's secret identity from a pool of possible candidates. Common wisdom is that using a binary search approach to narrow down candidates is the best strategy. In this work, I showed that this is NOT the case for the player who is behind. Instead, the player who is behind should make certain bold plays to maximize their chance to win. I was able to find an exact formula for these bold plays and prove their optimality. Published in Probability in the Engineering and Informational Sciences.

(With Mike Noyes & Jacob Funk) In this project, we considered a type of non-random TASEP-like evolution for particles on a finite line where particles deterministically move to the left under a simultaneous update rule. (This was presented in terms of binary strings in the paper). We found the limit law for the "stabilization time" for this update rule if you start with a random initial configuration. The limit law is Gaussian unless you start with a near-equal number of holes and particles...in which case an entirely different limit law is found. Published in the Journal of Theoretical Probability.
Below are notes I created from textbook material while studying for my Courant PhD Oral Exams. Here is a list of topics I looked at.
Below are final exam study sheets I created for courses I took:
Below are some miscellaneous notes that I have written up. They are mostly just the notes I have taken while studying someone else's lectures or written work. Be careful because these are rough notes and I'm sure there are many typos and errors!
Based on book by Patrick Billingsley
Based on notes by Terry Tao
Based on Chapter 1 of the book by Anderson, Guionnet, Zeitouni
Based on Chapter 3 of the book by Anderson, Guionnet, Zeitouni
Based on the book by Richard Stanley
Based on the book by D.A. Levin, Y. Peres & E.L. Wilmer
Based on the book written by Sidney I. Resnick
Based on a course given by Remco van der Hofstad
Based on notes written by Joel Spencer
Based on lectures given by Michel Ledoux
This is a survey of some basic results for PDEs, published in the Waterloo Mathematics Review.
My notes from the course "Limit Theorems II" taught by Henry McKean in Spring 2012 at CIMS
Courant Splash is an annual one-day lecture series at the Courant Institute of New York University, aimed at mathematically-inclined high school students in the New York metropolitan area.
The Fibonacci numbers are a famous sequence of numbers where
each number is given by the sum of the previous two numbers in the
sequence. Because of this recursive definition, it is not clear
how to calculate the 100th Fibonacci number without first
calculating the first 99.
This is the first version of the Fibonacci Numbers talk, an
updated version was presented in 2014.
Playing with randomness can lead to many situations that seem counter intuitive. One thing that is often surprising is how probabilities change when you are given some extra information. In this talk we will develop the tools we need to handle this and we will look at some examples where the results are surprising. The Monty Hall Problem is a famous example of the type of problem we will look at.
This talk is an updated version of the 2012 cSplash talk.
In this talk, we will use algebra to tackle the same problem as
2012 and learn more about the Fibonacci numbers.
We will also learn a neat trick to convert from miles to
kilometers using only the Fibonacci numbers.
This content was taught in both the Fall 2012 Workshop as well as the Spring 2014 Workshop