(These buttons explained below)
Question Corner and Discussion Area
A regular 18-sided polygon is inscribed in a circle, and triangles are formed by joining any 3 of the 18 vertices. How many obtuse triangles are there?Is this a question you have, or is it a question from an assignment or project that you are asking for help on? If it is an assignment or project question, you should really be asking us "here is a problem I am trying to solve and can't. I've tried . . . , but I'm stuck on . . . ; where can I go from here?" rather than simply asking us the same question that was asked of you. That helps us to answer more appropriately. It also makes it more likely that we will answer at all, for normally we don't answer questions that read as if they might be taken directly from an assignment or test, but we're always happy to answer questions about such problems and the concepts behind them. (In this case, though, the question is sufficiently non-standard that we will go ahead and answer it).
The real problem is that the question is ambiguous. There are two completely different possible interpretations, and therefore two completely different possible answers. We'll address each.
But first, here's an important characterization of obtuse angles: Suppose point B is on the arc of a circle going from A to C. Then angle ABC is obtuse if and only if the arc is less than a semicircle.
You can see this in two ways. First of all, there's a theorem in geometry which says that angle ABC is half the measure of the "other" arc from A to C (the one not containing B). Therefore, angle ABC is obtuse if and only if the other arc is more than 180 degrees, which is true if and only if the arc from A to C through B is less than 180 degrees (less than a semicircle).
You can also see it by remembering that any angle inscribed in a semicircle is a right angle. Now, if the arc from A to C through B is less than a semicircle, you can complete it into a semicircle ending at point D as shown below. Then angle ABD is a right angle, and it is clear from the picture that angle ABC is greater than angle ABD and therefore obtuse. This shows that if the arc is less than a semicircle the angle ia obtuse; you can draw similar pictures which show that, if the arc is more than a semicircle, the angle is acute.
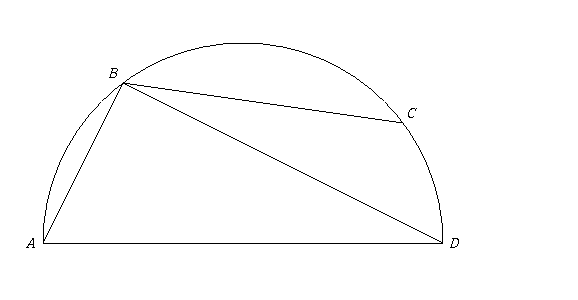
Now here are the two interpretations of the question, and their solutions:
Interpretation #1. You choose any 3 of the 18 vertices, call them A, B, and C, and join them. How many obtuse triangles are formed by this process?
First, here's a convenient way to describe the relative positions of the vertices. Let's label the vertices A, B, and C in order clockwise around the polygon. Starting at A and moving clockwise, count how many edges there are from A to B, from B to C, and from C to A. The total of these three numbers will always be 18, since by the time you get back to A you have covered all 18 edges.
For example, if A is at vertex 1 of the 18-gon, B is at vertex 7, and C is at vertex 11, the three numbers will be 6, 4, and 8.
The triangle ABC is obtuse if and only if A, B, and C all lie on some arc which is less than a semicircle (i.e., encompasses fewer than 9 vertices of the polygon). This is the same as saying that two of the three numbers add up to less than 9, which is equivalent to the third number being greater than 9.
Therefore, triangle ABC is obtuse if and only if one of the three numbers is greater than 9.
(In fact, you can say more than this. Suppose the three numbers are (a,b,c). The angle at vertex B equals half the measure of the arc from C to A that doesn't include B. This arc encompasses c edges. Each edge corresponds to an angle of 360/18 = 20 degrees, so the arc from C to A is 20c degrees, so angle B is half that, namely 10c degrees. Similarly, angle C is 10a degrees and angle A is 10b degrees. For example, if the three numbers are 3, 5, and 10, that means the angles of triangle ABC are 50, 100, and 30 degrees. This shows that ABC is obtuse if and only if one of the numbers is greater than 9).
Now the only question is, how many other triangles are there? You get an extra triangle each time one of the lines you drew combines with two polygon edges to form a triangle. This happens every time you draw a line between two vertices that are separated by only 2 edges: in other words, it happens every time one of the three numbers is a "2".
You should be able to easily see that each of these "extra" triangles is obtuse (one of its angles is the angle between two edges of the 18-gon, which is 160 degrees).
Therefore, the number of obtuse triangles equals the number of "extra" triangles (which is the number of 2's among the three numbers), plus 1 if the "main" triangle ABC is obtuse (which happens if one of the three numbers is a 9).
You should be able to convince yourself that this means the number of obtuse triangles equals the number of 2's and 9's among the 3 numbers, and that this can be anywhere from 0 to 3, depending on how the vertices A, B, and C were chosen.
Interpretation #2. For any possible choice of three vertices A, B, and C, you draw the triangle ABC. Thus you have drawn 816 triangles in all (that's the number of ways of choosing 3 out of 18 things). How many of these 816 triangles are obtuse?
Label the vertices of each obtuse triangle A, B, and C, in order clockwise, starting at the vertex before the obtuse angle (so that angle B is the one which is obtuse).
Let's ask ourselves, "Suppose we know where vertex A is. Where could vertices B and C be?" In order for angle B to be obtuse, the clockwise arc from A through B to C must be less than a semicircle, so vertex C must come before the 9th vertex after A.
Therefore, B and C could be anywhere among the next 8 vertices after A. The number of possible choices for B and C equals the number of ways of choosing a pair of vertices out of 8 possibilities.
This means that for each of the 18 possible positions for vertex A, there are x different obtuse triangles with A at that position, where x is the number of ways of choosing two out of eight things.
You should be able now to figure out the rest of the answer.
Go backward to Angle Between Vertices of a Tetrahedron Go up to Question Corner Index Go forward to Fractals and their History Switch to text-only version (no graphics) Access printed version in PostScript format (requires PostScript printer) Go to University of Toronto Mathematics Network
Home Page